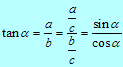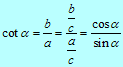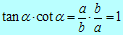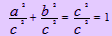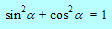KOTNE FUNKCIJE
Za začetek narišimo ostri kot in nekaj pravokotnic na vodoravni krak tega kota:
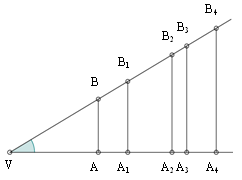
Pravokotni trikotniki VAB, VA1B1, VA2B2,
VA3B3 in VA4B4, ki pri tem nastanejo,
so podobni; imajo namreč enake kote. Zato so razmerja dveh enakoležnih stranic pri vseh trikotnikih
enaka. Ta razmerja se lahko spremenijo le, če spremenimo kot - torej so odvisna le od kota. V
matematiki pa takim odvisnim količinam rečemo funkcije. Ker so razmerja stranic v pravokotnem
trikotniku odvisna le od kota, jih imenujemo kotne funkcije.
Vseh razmerij po dveh stranic v pravokotnem trikotniku je šest, vendar večinoma uporabljamo samo štiri,
to so:
sinus, kosinus, tangens in kotangens kota.
DEFINICIJA:
|
|
|
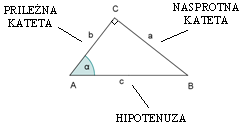
Sinus kota α je enak razmerju med kotu α nasprotno kateto
in hipotenuzo.
|
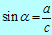
|
|
Kosinus kota α je enak razmerju med kotu α priležno kateto
in hipotenuzo.
|
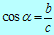
|
|
Tangens kota α je enak razmerju med kotu α nasprotno
kateto in priležno kateto.
|
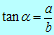
|
|
Kotangens kota α je enak razmerju med kotu α priležno in
nasprotno kateto.
|
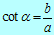
|
(Tangens lahko označimo tudi s tg, kotangens pa s ctg.)
Obstajata tudi funkciji sekans 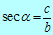 in
kosekans
in
kosekans 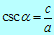 , ki pa se v praksi ne uporabljata.
, ki pa se v praksi ne uporabljata.
ZVEZE MED KOTNIMI FUNKCIJAMI
Če v definiciji funkcije tangens v pravokotnem trikotniku ABC ulomek a/b razširimo s številom 1/c,
dobimo prvo povezavo:
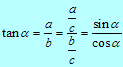
Na enak način dobimo drugo povezavo:
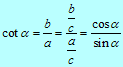
Naslednja povezava je:
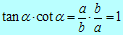
Zadnjo povezavo dobimo, če enačbo za Pitagorov izrek (glej poglavje o izrekih, kjer lahko najdeš Pitagorov izrek) delimo s c2:
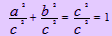
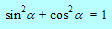
Do vrednosti kotnih funkcij lahko na enostaven način pridemo le za kote 0°, 30°, 45°, 60° in 90°, pri
drugih primerih pa si najlažje pomagamo z žepnim računalom.
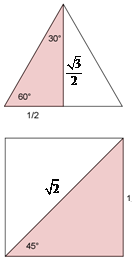
Natančne vrednosti kotnih funkcij kotov 30° in 60° dobimo iz polovice enakostraničnega trikotnika s stranico dolžine 1, za
kot 45° pa iz polovice kvadrata s stranico dolžine 1. (Da je višina enakostraničnega trikotnika s stranico dolžine 1 enaka √3/2 je dokazano
v poglavju o ploščinah in obsegih trikotnika. Da je dolžina diagonale kvadrata s stranico dolžine 1 enaka √2 pa sledi iz
Pitagorovega izreka, ki ga najdemo v poglavju o izrekih.)
|
|
Natančne vrednosti za naštete kote zapišemo v tabelo, zelo koristno pa je, da se jih naučimo na
pamet.
Natančne vrednosti kotnih funkcij za nekatere kote:
| α°
| 0° |
30° |
45° |
60° |
90° |
| sin α |
0 |
1/2 |
√2/2 |
√3/2 |
1 |
| cos α |
1 |
√3/2 |
√2/2 |
1/2 |
0 |
| tan α |
0 |
√3/3 |
1 |
√3 |
∞ |
cot α |
∞ |
√3 |
1 |
√3/3 |
0 |
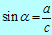
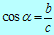
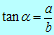
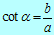

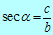 in
in
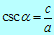 , ki pa se v praksi ne uporabljata.
, ki pa se v praksi ne uporabljata.