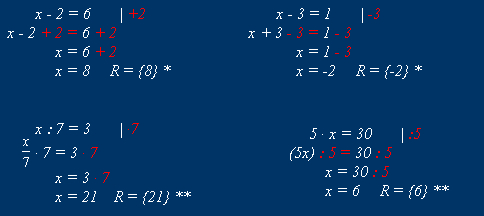Enačba.
Osnovna množica. Množica rešitev
Kratka ponovitev
Dogovorimo se:
- Vrednosti neznanke, pri katerih je enačba smiselna, sestavljajo osnovno
množico U.
- Število ali števila, ki so rešitev dane enačbe in so hkrati tudi elementi
osnovne množice, sestavljajo množico rešitev R.
1. primer:
Rešimo enačbo x + 5 = 3 najprej za
U =  , nato
pa še za U =
, nato
pa še za U =  .
.
Rešitev enačbe x + 5 = 3 je celo število -2. Ker -2 ni
naravno število, enačba v množici naravnih števil nima rešitve. Rešljiva pa je v
osnovni množici celih števil. Njena rešitev je x = -2. Zapišimo jo še z
množico R = {-2}.
2. primer:
S poskušanjem rešimo enačbo 2·x
+ 8 = 2 (x + 4) za U =
 .
.
| x |
2·x
+ 8 = 2 (x + 4) |
p/n |
| 1 |
2·1
+ 8 = 2 (1 + 4) |
p |
| 2 |
2·2
+ 8 = 2 (2 + 4) |
p |
| 3 |
2·3
+ 8 = 2 (3 + 4) |
p |
| 4 |
2·4
+ 8 = 2 (4 + 4) |
p |
| 5 |
2·5
+ 8 = 2 (5 + 4) |
p |
Enačba ima toliko rešitev, kolikor je
števil v osnovni množici. Za vsako število iz osnovne množice, dobimo pravilno
izjavo. Množica rešitve te enačbe je enaka osnovni množici R = U =
 .
.
Enačbe te vrste imenujemo identične enačbe ali identitete.
3. primer:
Linearne enačbe z eno neznanko rešimo z ekvivalentnim
preoblikovanjem. Vse člene z neznanko spretno prenesemo na eno stran
enačaja, vse preostale pa na drugo.
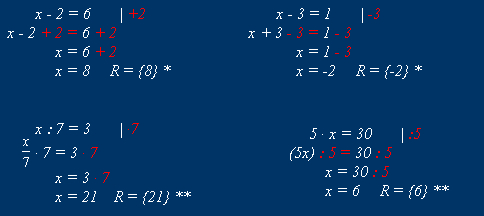
* Za vsako realno število a, b in c velja: če
a = b, potem a + c = b + c
** Za vsako realno število a, b in c, c  0
velja: če a = b, potem a ·
c = b ·
c
0
velja: če a = b, potem a ·
c = b ·
c
4. primer:
Z zaporedno uporabo pravil o preoblikovanju
enačb rešimo naslednjo enačbo:
 |
- 7 = 2
| + 7 |
 |
- 7 + 7 = 2 + 7 |
 |
= 2 + 7 |
 |
= 9
|
·
7 |
 |
·
7 = 9 · 7 |
| x |
= 63
R = {63} |
5. primer:
Rešimo kvadratno enačbo x2 = 36:
Njeni rešitvi sta x1 = 6 in x2 = -6. Torej R
= {6, -6}.
6. primer:
Rešimo še kvadratno enačbo (x - 3)(x - 5) = 0.
Rečemo ji tudi razcepna enačba.
Rešujemo jo s sklepanjem: x - 5 = 0 ↔ x =
5
x - 3 = 0 ↔ x = 3
Produkt dveh izrazov je enak 0, če je vsaj eden od obeh faktorjev enak
0. Torej R = {5, 3}
|
Rešitev ali koren enačbe je vsako število iz osnovne množice
U, pri katerem sta vrednosti izrazov na levi in desni strani enačbe
enaki.
Vse rešitve enačbe sestavljajo množico rešitev R dane enačbe.
Ekvivalentno preoblikovanje enačb:
1. Na obeh straneh enačbe lahko prištejemo ali od obeh strani
odštejemo isto število ali izraz.
2. Obe strani enačbe lahko pomnožimo ali delimo z istim, od
nič različnim številom ali izrazom.
Glede na stopnjo neznanke delimo enačbe na:
linearne enačbe ali enačbe prve stopnje, kvadratne enačbe
ali enačbe druge stopnje in enačbe višjih stopenj.
Glede na število neznank delimo enačbe na enačbe z eno, dvema ali
več neznankami.
Enačbe so lahko:
- ekvivalentne: te imajo različno obliko, a enako množico rešitev
- identične: so enačbe, pri kateri je osnovna množica U hkrati
množica njihovih rešitev, U = R
- rešljive: imajo največ toliko rešitev, kolikršna je stopnja
neznanke
- nerešljive: te nimajo nobene rešitve |
NAZAJ