Galileo GALILEI je podal svojo rešitev problema brahistohrone leta 1638, še preden je Bernulli problem sploh eksplicitno zastavil. Objavil jo je v Tretjem delu svoje Razprave o dveh novih znanostih. Tu je tudi naredil primerjavo med enakomernim in enakomerno (naravno) pospešenim gibanjem. Pokazal je, da je dolžina poti padajočega telesa sorazmerna kvadratu časa padca. S pomočjo tega dejstva je prišel do naslednjega zaključka:

Izrek: Časa spustov vzdolž dveh ravnin različne dolžine, naklona in višine sta med seboj v razmerju, ki je enako produktu razmerja njunih dolžin in kvadratnega korena obratnega razmerja njunih višin.

To razmerje sledi iz ugotovitve, da telo prepotuje razdaljo L in se spusti za višino H v času t, za katerega velja:

Galileo je nato dokazal naslednji izrek:

Izrek: Če z najvišje ali najnižje točke navpičnega kroga narišemo poljubno nagnjeno ravnino, ki seka obod, potem so časi spusta vzdolž teh daljic med seboj enaki.

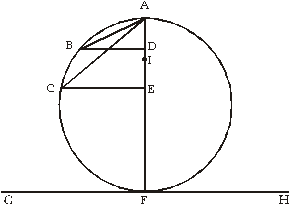
Na vodoravno premico GH postavi navpičen krog. Iz njegove najnižje točke – točke, kjer se krog dotika vodoravnice – nariši premer FA in iz najvišje točke A nariši ravnine, nagnjene do B in C, ki sta poljubni točki na obodu, časi spusta vzdolž le-teh so potem enaki.

Dokaz: Nariši BD in CE pravokotno na premer in naj bo AI geometrijska sredina višin AE in AD; in ker so pravokotniki FA.AE in FA.AD enaki kvadratom AC oziroma AB, medtem ko je pravokotnik FA.AE proti pravokotniku FA.AD v enakem razmerju, kot je AE proti AD, sledi, da je kvadrat AC proti kvadratu AB v enakem razmerju, kot je dolžina AE proti dolžini AD. Toda, ker je dolžina AE proti AD, kot je kvadrat AI proti kvadratu AD, sledi, da sta kvadrata na daljicah AC in AB drug proti drugemu, kot sta kvadrata na daljicah AI in AD. Torej je tudi dolžina AC proti dolžini AB, kot je AI proti AD. Toda predhodno je bilo pokazano, da je razmerje časov spusta vzdolž AC proti tistemu vzdolž AB, enako produktu dveh razmerij, AC proti AB in AD proti AI. Toda omenjeno razmerje je enako razmerju AB in AC. Zato je razmerje časov spusta vzdolž AC in vzdolž AB enako produktu razmerij AC proti AB in AB proti AC. Razmerje teh časov je torej ena. Od tod sledi naš izrek.

Galileo se je ukvarjal tudi s problemom določitve naklona ravnine, po kateri dosežemo izbrano navpično ravnino v najkrajšem času, če začnemo iz mirovanja v točki A. S pomočjo prejšnjega izreka ugotovimo, da je optimalni kot 45°.

Dokazal pa je tudi naslednji izrek, v katerem pojasni, kako je mogoče čas spusta med dvema točkama, ki ležita na daljici z naklonom 45°, še izboljšati.

Izrek: Če iz najnižje točke navpičnega kroga napnemo tetivo, pod katero je lok, ki ni večji od kvadranta, in če iz krajišč iste tetive narišemo dve drugi tetivi do poljubne točke na loku, potem bo čas spusta vzdolž slednjih tetiv krajši kot vzdolž prve in tudi krajši, za isto vrednost, kot vzdolž spodnje od slednjih dveh tetiv.

Od tod pa je Galileo sklepal, da je krožni lok krivulja najhitrejšega spusta:

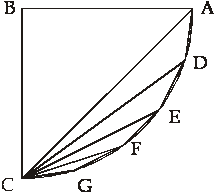
Trditev: Iz povedanega lahko sklepamo, da pot najhitrejšega spusta iz ene točke v drugo ni najkrajša pot, ki je daljica, ampak krožni lok. V kvadrantu BAEC z navpičnico BC, razdeli lok AC v poljubno število enakih delov AD, DE, EF, FG ter GC in iz točke C nariši daljice do točk A, D, E, F in G. Prav tako nariši daljice AD, DE, EF, FG in GC. Očitno je spust po poti ADC časovno krajši kot spust vzdolž AC ali spust vzdolž DC iz mirovanja v D. Toda telo, ki začne iz mirovanja v A, bo prečkalo pot DC hitreje kot pot ADC medtem ko, če krene iz mirovanja v A, bo prečkalo pot DEC hitreje ko samo pot DC. Torej je spust vzdolž treh tetiv ADEC hitrejši kot vzdolž dveh tetiv ADC. Podobno, če spremljamo spust vzdolž ADE, je čas, potreben za prečenje vzdolž EFC, krajši kot vzdolž samega EC. Torej je spust vzdolž štirih tetiv ADEFC hitrejši kot spust vzdolž treh tetiv ADEC. In končno bo telo po spustu vzdolž ADEF hitreje prečkalo dve tetivi FGC kot eno samo FC. Torej je spust vzdolž petih tetiv ADEFGC hitrejši od tistega vzdolž štirih ADEFC. Posledično, bližje kot je opisani poligon krogu, krajši je čas spusta iz A v C.