Prva naloga je le različica Hipokratove prve uspešne kvadrature lune in lahko srečamo v različnih knjigah in učbenikih.
Rahla posplošitev Hipokratovega sklepa sta druga in tretja naloga, ki jo je okrog leta 1000 zastavil in rešil Hasan Ibn al Haitam (Ibn al-Haytham), znan tudi kot Alhazen, kar je latinizirana oblika njegovega imena. Zanimivo je, da jo je približno pet stoletij kasneje, verjetno neodvisno, rešil tudi Leonardo da Vinci. Med njegovimi rokopisi so namreč našli številne skice na to temo.
Če torej uspešno rešimo drugo in tretjo nalogo, kvadriramo dve luni hkrati.
Vrnimo se h kvadraturi ene same lune. V prvem Hipokratovem primeru je krožni odsek, ki ga določa zunanji lunin lok, ravno polovica kroga. Toda Hipokrat je poleg tega našel še dva druga primera polmesecev, ki ju lahko kvadriramo; pri enem je krožni odsek večji, pri drugem pa manjši od polovice kroga. Na žalost so ta dva njegova rezultata spregledali, ju v 18. stoletju ponovno odkrili in šele kasneje ugotovili, da ju je poznal že Hipokrat.
Pri drugem Hipokratovem polmesecu je središčni kot zunanjega loka večji od 180°. Do njegove konstrukcije pridemo po naslednjem postopku:
Najprej narišemo tak enakokraki trapez τ z osnovnico a, krakoma b in vzporedno osnovnico c = b, da velja a2 = 3b2. Trapez τ naj ima oglišča A, B, C, D, pri čemer naj bosta AB in CD osnovnici, BC in AD pa kraka. Temu trapezu očrtajmo krog. Tako dobimo zunanji lok ADCB polmeseca, notranji lok pa naj bo podoben loku nad stranico DC (slika 2).
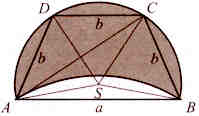
Slika 2.
Če sledimo Hipokratovim navodilom, se nam porodi kar nekaj vprašanj, ki si jih lahko zastavimo v obliki naslednjih štirih nalog:
Tretja Hipokratova konstrukcija, pri kateri je zunanji lok manjši od 180°, je nekoliko bolj zapletena.
Načrtajmo polkrožnico nad premerom AC. Točka B naj bo njeno središče, s pa simetrala daljice BC. Nato položimo skozi točko C premico, ki seka simetralo s v točki E in polkrožnico v točki F, pri čemer naj velja FE2 = 3/2FB2 (slika 3).
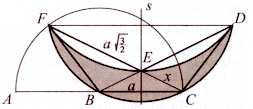
Slika 3.
Kako to storimo, je poseben problem, povezan z geometrijskim reševanjem kvadratne enačbe. Naj bo BC = a in CE = x. Potem zaradi podobnosti trikotnikov FBC in BCE velja CF · CE = BC2, se pravi (x + √(3/2)a)x = a2 oziroma x2 + √(3/2)ax - a2 = 0. Če poznamo x, lahko konstruiramo točko E in nato še točko F.
Točko F prezrcalimo preko simetrale s tako, da dobimo še točko D, in enakokrakemu trapezu FBCD očrtajmo krog. Nato narišimo še krožni lok DEF tako, da dobimo polmesec FBCDE (slika 3).
Od tod lahko dobimo naslednje naloge:
Poleg teh treh glavnih primerov kvadriranja lun je Hipokratu uspelo kvadrirati tudi eno od lun in krog skupaj.
Načrtajmo koncentrična kroga kroga s polmeroma r in R tako, da je R2 = 6r2, in vsakemu od njiju včrtamo pravilni šestkotnik, poleg tega pa nad krajšo diagonalo večjega narišimo podoben lok, kot je nad vsako stranico (slika 4).
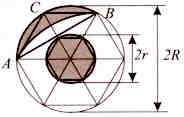
Slika 4.
Zanimivo je, da so nekaj časa prav zaradi tega Hipokratovega uspeha zmotno mislili, da mu je uspela kvadratura kroga, češ, če zna kvadrirati luno, poleg tega pa še luno in krog, zna kvadrirati tudi krog. Pri tem so spregledali, da pri obeh rešitvah ne gre za isto luno.
Tako si lahko zastavimo naslednji dve nalogi:
Zgodba o Hipokratovih lunah pa se ni zaključila v antiki, niti ne v srednjem veku ali renesansi, ampak v 20. stoletju. Če hočemo vsaj na kratko opisati, kaj se je zgodilo, moramo dati problemu kvadrature lune drugačno, trigonometrično obliko.
Oglejmo si poljuben lunin krajec, katerega zunaji lok pripada krogu s polmerom r in središčnemu kotu 2θ, notranji lok pa krogu s polmerom R in središčnemu kotu 2φ (slika 5).
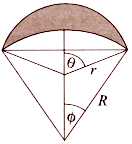
Slika 5.
Da se pokazati, da če kote merimo v radianih, za ploščino p luninega krajca na sliki 5 velja naslednja formula:
p = r2θ - R2φ + 1/2(R2sin 2φ - r2sin 2θ).
Če se omejimo samo na primer, ko sta ploščini obeh krožnih izsekov enaki, se pravi, ko je r2θ = R2φ, se formula nekoliko poenostavi:
p = 1/2(R2sin 2φ - r2sin 2θ).
Denimo, da je v takem primeru razmerje med središčnima kotoma enak racionalnemu številu k, torej je θ = kφ. Potem je R = r√(k) in ploščina lune p = r2(k sin 2φ - sin 2kφ)/2. Ker pa vedno velja r sin φ = R sin θ, saj tako leva kot desna stran pomenita polovico iste lunine tetive (glej sliko 5), so za kot φ možne le tiste vrednosti, pri katerih je
sin kφ = √(k) sin φ.
To je v splošnem kar zapletena enačba. V posebnih primerih racionalnih števil k pa se na srečo kar precej poenostavi, tako da za sin φ dobimo enačbo, iz katere lahko samo s kvadratnimi koreni in štirimi računskimi operacijami izrazimo sin φ. Kot je dobro znano, lahko tedaj sin φ, oziroma potem tudi sam kot φ konstruiramo samo z ravnilom in šestilom. To pa pomeni, da lahko tudi lunin krajec nad dano tetivo (ali z danim zunanjim ali notranjim polmerom) konstruiramo le z evklidskim orodjem. Formula za ploščino pove, da lahko enako konstruiramo tudi vrednost za p oziroma ploščinsko enak kvadrat. Torej lahko v takem primeru upravičeno govorimo, da je kvadratura lune uspela.
Tri Hipokratove primere dobimo, če vzamemo k = 2, k = 3 ali k = 3/2.
Vse to si lahko ogledamo v naslednjih dveh nalogah:
Nadaljna dva primera, ko je kvadratura lune možna, je našel M. J. Wallenius leta 1766, in sicer za k = 5 in k = 5/3. T. Clausen pa je leta 1840 ponovno rešil primere k = 3, 3/2, 5, 5/3 (tedaj še ni bilo znano, da je primera k = 3 in k = 3/2 poznal že Hipokrat). Postavil je tudi domnevo, da razen teh in prve Hipokratove kvadrature (k = 2) ni drugih primerov uspešnega kvadriranja lune pri racionalnem razmerju središčnih kotov. Raziskovanje problema se je nadaljevalo v 20. stoletju. E. Landau je leta 1903 raziskal problem brez predpostavke, da je razlika med ploščinama krožnih izsekov, to je med r2θ in R2φ, enaka 0, ampak je enak ploščini, ki je konstruktibilno število (se pravi, da jo lahko izrazimo iz števila 1 samo z racionalnimi operacijami in kvadratnimi koreni). Pokazal je, da ta razširitev ne pripelje do novih primerov kvadriranja. Istočasno je podal tudi dokaz, da za liho praštevilo k kvadratura ni možna, če k ni Fermatovo praštevilo (to je praštevilo oblike k = 22j + 1, j = 0, 1, 2,...). Leta 1929 je L. Čakalov dokazal Landauvov izrek na krajši način in prispeval še neskončno drugin primerov, ko kvadratue ni. Seveda je bilo to še daleč od dokaza, da je kvadratura možna le v omenjenih petih primerih. Prvi pozitivni rezultat je leta 1934 prispeval N. Čebotarev, ki je Clausenovo domnevo potrdil za primer k = m/n, kjer sta m in n tuji lihi števili: izmed takih števil je kvadratura možna le za k = 3/1 = 3, k = 5/1 =5 in k = 5/3. Pri tem je uporabljal teorijo tako imenovanih p-adičnih števil. Problem je dokončno rešil šele A. V. Dorodnov leta 1947 z detajlno proučitvijo preostalega primera, ko je eno od števil m, n liho, drugo pa sodo. S tem je bila Clausenova domneva v celoti potrjena, zgodba o Hipokratovih lunah pa zaenkrat zaključena.