Snov tega razdelka lahko opredelimo kot zabavno matematiko, čeprav je uporabna v mnogih praktičnih nalogah.

Pobližje si bomo ogledali Eulerjeve in Hamiltonove grafe, njihove temeljne značilnosti in zakonitosti . Snov je primerna za vse, ki jih zabavna matematika zanima, saj predhodno znanje ni potrebno.

Bolj ali manj bomo ves čas obravnavali dva problema:

• Prvi je raziskovalčev problem, kjer bi raziskovalec rad pregledal vse ceste med številnimi mesti. To bi rad storil tako, da bo vsako cesto prehodil največ enkrat in se ponovno vrnil v mesto, kjer je svojo pot začel.
• Drugi problem je popotnikov. Popotnik bi rad obiskal določena mesta, vendar tako, da bo vsako mesto obiskal natanko enkrat in zopet končal v izhodiščni točki (mestu).

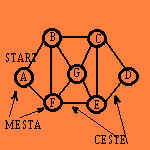
Za boljše razumevanje obeh problemov, si oglejmo zgornjo sliko. Za začetno točko si vzemimo kar točko A (mesta so na sliki označena s črkami).

Raziskovalec mora poiskati tak obhod, ki se začne v A in gre po vsaki cesti (povezavi) natanko enkrat ter konča zopet v A. Možnosti za tak obhod je več, pa si jih oglejmo le nekaj:

• ABFGBCGECDEFA

• ABCDEFBGCEGFA

• AFBGFEGCEDCBA

• AFGCDEGBCEFBA

Tudi popotnik želi poiskati obhod, ki se začne in konča v A, vendar (za razliko od raziskovalca) gre on natanko enkrat skozi vsako mesto. Poglejmo si, kakšno zaporedje bi si moral izbrati on:

• ABGCDEFA

• ABCDEGFA

• AFGEDCBA

• AFEDCGBA

Kot vidimo, potuje raziskovalec po vsaki povezavi natanko enkrat, mesta pa lahko obišče po večkrat, medtem ko mora popotnik obiskati vsako mesto natanko enkrat, ni pa mu treba potovati po vseh cestah (povezavah).

Če si sedaj zgornjo sliko pogledamo kot graf, kjer so točke označene s črkami mesta, povezave pa so ceste med njimi, lahko oba problema zapišemo takole: problem raziskovalca je poiskati enostaven obhod, na katerem so vse povezave grafa, popotnikov problem pa je poiskati cikel, na katerem so vse točke grafa.  

Zapišimo sedaj nekaj definicij za pojme, na katere smo že naleteli:

• Graf  G  je neprazna množica elementov, ki jih imenujemo točke in seznam parov teh točk, ki jih imenujemo povezave.

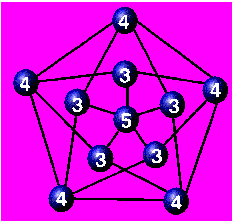
          Primer grafa:

• Zanka grafa  je povezava, ki se začne in konča v isti točki.

• Stopnja točke:  Vzemimo nek graf G brez zank. Potem je stopnja točke  število povezav, ki vodijo iz (oziroma v) te točko. Stopnjo točke v označimo z deg v.

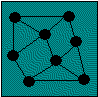
          Oglejmo si stopnje točk na naslednjem grafu (za večjo sliko klikni na graf):

• Graf G je  povezan,   če obstaja povezava med poljubnim parom točk, sicer je  nepovezan.

• Sprehod  v grafu G je zaporedje povezav, ki jih "prehodimo". Če so vse povezave sprehoda različne, ga imenujemo  enostavni sprehod.

• Obhod  je sprehod v grafu, pri katerem začetna in končna točka sovpadata. Enostavni obhod  je obhod, v katerem so vse povezave različne.

• Povezani graf je Eulerjev, če obstaja enostaven obhod, na katerem so vse povezave grafa. Tak obhod imenujemo Eulerjev obhod.

• Povezani graf je Hamiltonov, če obstaja cikel, na katerem so vse točke grafa. Tak cikel imenujemo Hamiltonov cikel.

V nadaljevanju si bomo oba tipa grafov ogledali še bolj podrobno (potrebne in zadostne pogoje, da je nek graf Eulerjev oziroma Hamiltonov). Pokazali bomo tudi zvezo med Eulerjevimi grafi in na primer problemom čiščenja snega mestnih ulic, iskanjem poti iz labirinta,... ter Hamiltonovimi grafi in šahovskim problemom,....