Linearne preslikave v ravnini

Ta sestavek je zamišljen kot učna ura za gimnazijce, ki jih matematika še posebej zanima! Upam pa, da bo prišla prav še komu drugemu, na primer študentom, ki spoznavajo osnovne pojme iz linearne algebre. Štart pri dvorasežnih matrikah je več kot primeren!

Med najpomembnejše preslikave gotovo sodijo linearne preslikave. Pojavljajo v vseh mogočih vejah in panogah matematike, najdemo jih pa tudi v fiziki, elektrotehniških vedah, računalništvu, ekonomiji in še kje. Linearna preslikava je preslikava A definirana na nekem vektorskem prostoru, ki zadošča naslednjim pravilom:

A(x+y) = Ax+Ay, za vsaka vektorja x in y;
in
A(k x) = k Ax, za vsak vektor x in skalar k;

kodomena take preslikave pa je spet nek vektorski prostor. Nas bodo konkretno zanimale le linearne preslikave, ki slikajo iz (realne) ravnine R2 nazaj vase. Take linearne preslikave bomo imenovali tudi "operatorji". Takoj istaknimo najpomembnejše dejstvo, ki bo rdeča nit tega sestavka:

Izrek. Linearna preslikava je enolično določena s slikami baznih vektorjev. Torej, če poznamo sliki baznih vektorjev, potem vemo kako operator deluje na poljubnem vektorju.

Oglejmo si konkreten primer. Vemo, da vektorja e1 = (1,0) in e2 = (0,1) tvorita (standardno) bazo v ravnini in naj bo A tak operator, da je Ae1 = (-1,2) in Ae2 = (3,0). Tedaj je slika vektorja (-3,7) enaka A(-3,7) = A(-3e1 + 7e2) = A(-3e1) + A(7e2) = -3Ae1 + 7Ae2 = -3(-1,2) + 7(3,0) = (24,-3).

Kot je razvidno je tak način računanja, precej zamudno. Delo si olajšamo z idejo matrike. Naj bosta e in f poljubna bazna vektorja v ravnini in A operator. Sestavimo iz slik Ae = (a,b) in Af = (c,d) baznih vektorjev takole kvadratno shemo:

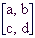
ki ji pravimo matrika opertorja A glede na izbrano bazo. Taka matrika določa operator enolično, računanje z njo pa je kaj priročno:

kjer je (x,y) poljuben vektor. Za pokušino, poišči matriko, ki pripada operatorju iz prejšnjega primera, ter sliko vektorja (-3,7). Matrike bomo oznčevali tudi s tole "kompaktno" pisavo: [[a,b],[c,d]]. Matrike (oziroma operatorje) lahko tudi med seboj seštevamo in množimo, po pravilih:

in

Med posebej "imenitnimi" matrikami moramo omeniti vsaj dve. To sta:

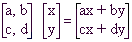
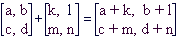
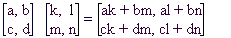
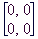
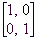
Ti dve matriki, bomo vseskozi označevali z 0 (ničelna matrika) in I (identiteta). Računanje z njima pa je kaj enostavno. Če prvi prišteješ neko matriko A, dobiš nazaj matriko A in če matriko I pomnožiš z A dobiš nazaj spet matriko A.

Na matrike lahko gledamo tudi kot na posplošitev pojma števila. Pri tej interpretaciji matrik, se seveda vprašamo, ali imajo tudi matrike take lastnosti kot števila. Na primer: Vemo, da za vsako neničelno število a obstaja njegov inverz, to je tako stevilo b, da je ab = 1. Te lastnosti matrike nimajo. Vzemimo neničelno matriko A = [[0,1],[0,0]]. Ni se težko prepričati, da za to matriko ne obstaja taka matrika B, da bi veljalo AB = I (matrika I ima (prevzeme) to lastnost pri matrikah, ki jo ima 1 pri številih). Take matrike, ki pa zadoščajo tej lastnosti imenujemo obrnljive matrike. S stališča linearnih preslikav, pomeni to, da je preslikava, določena z obrnljivo matriko, injektivna. V primeru linearnih preslikav je to ekvivalentno bijektivnosti in surjektivnosti. Seveda nas zanima kdaj pa je neka matrika obrnljiva. V ta namen definiramo pojem determinante matrike, ki je opredeljena s predpisom:

det(A) = ad - bc,

kjer je A matrika [[a,b],[c,d]]. Iskaže se, da je matrika obrnljiva, natanko tedaj, ko je njena determinanta neničelna (poskusi dokazati). Drug kriterij za ugotavljanje obrnljivosti matrike dobimo s pojmom ranga matrike. Spomnimo se, da je matrika sestavljena iz slik baznih vektorjev. Število linearno neodvisnih slik baznih vektorjev je po definiciji rang matrike. Od tod vidimo, da je matrika obrnljiva, če je njen rang enak 2. In kakšna je inverzna matrika? Če je matrika A = [[a,b],[c,d]] obrnljiva, je njen inverz:

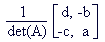
Imajo pa matrike nekatere lastnosti, ki jih števila nimajo. Na primer, med (realnimi) števili ne najdemo takega, katerega kvadrat bi bil -1. Toda kvadrat matrike [[0,1],[1,0]], pa je natanko -I (relacijo med 1 in I smo že pojasnili). Za nalogo poskušaj poiskati še nekaj lastnosti, ki jih matrike imajo (nimajo) in števila nimajo (imajo).

Končajmo prvi del tega sestavka z nekaj primeri posebej odlikovanih matrik. Matrikam oblike:

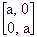
pravimo skalarne matrike in so "prava" posplošitev pojma števil. Take matrike označujemo kar s skalarjem, ki nastopa na diagonali, to je v zagornjem primeru število a (kar smo že storili, pri inverzni matriki), ali pa z aI, kar pomeni, da je skalarni večkratnik matrike I.

Naslednja družina matrik so diagonalne matrike:

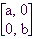
Vidimo, da so skalarne matrike le poseben primer diagonalnih matrik. Eno najbolj znamenitih vprašanj v matematiki je ali je vsak linearen operator v neki bazi predstavljiv z diagonalno matriko. Odgovor je negativen. Konkreten primer pa je operator, ki je v standardni bazi predstavljen z matriko: [[1,1][0,1]]. Seveda pa ostaja vprašanje kateri operatorji pa so predstavljivi z diagonalnimi matrikami. Preden citiramo ta izrek, povejmo, da je matrika transponirana k matriki M = [[a,b],[c,d]] definirana z

in jo označimo z M'.

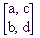
Izrek. Linearna preslikava, ki je prestavljena v neki bazi z matriko M, je predstavljiva z diagonalno matriko natanko tedaj, ko velja: MM' = M'M. Takim operatorjem pravimo normalni operatorji, matrikam pa normalne matrike. To trditev poznamo v literaturi, kot spektralni izrek.

Poseben primer normalnih matrik predstavljajo simetrične matrike. To so matrike oblike:

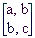
Ni se težko prepričati, da je taka matrika normalna. Zaključimo s tem, da za simetrično matriko M velja: M = M', torej je enaka svoji transponiranki.

Literatura