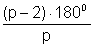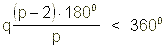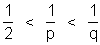PET PLATONOVIH TELES
Euklidovo ravnino lahko zapolnimo s kvadrati (regularno tlakovanje) s štirimi v vsakem vrhu. Če si prizadevamo, da so kvadrati po trije skupaj v vsakem vrhu, dobimo figuro podobno figuri, ki bi jo dobili, če bi uporabili 6 kvadratov in imamo kocko. Podobno lahko ravnino zapolnimo s pravilnimi trikotniki, s po šest v vsakem vrhu in je zelo zanimivo, da bi videli, kaj se zgodi, če so samo trije v vrhu, štirje ali pa pet namesto šestih. Druga možnost bi bila, da bi uporabili petkotnike, v vsakem vrhu tri. Z možnimi pričakovanji, da na podoben način lahko zapolnimo tudi sfero, je polieder najpreprostejše telo.
1. PIRAMIDE, PRIZME IN ANTIPRIZME
Konveksen poligon bi lahko opisali kot končno področje ravnine »ograjeno« s končnim številom črt, v smislu, da njegova notranjost leži znotraj na vsaki strani posamezne črte. Analogno je konveksen polieder končno območje prostora znotraj končnega števila ravnin. Del vsake ravnine, ki je odrezan od drugih ravnin je poligon in ga imenujemo lice. Skupni del dveh lic je rob. Najbolj vsakdanji poliedri so piramide in prizme. Mi se bomo ukvarjali samo s »pravilnimi regularnimi« piramidami, katerih lica so sestavljena samo iz regularnih n-poligonov in n-enakokrakih trikotnikov in s »pravilnimi regularnimi« prizmami, ki imajo lica sestavljena iz dveh regularnih n-poligonov povezanih z n-pravokotniki (tako sta dva pravokotnika in en n-poligon v vsakem vrhu).
Višina vsake take prizme je ponavadi prilagojena tako, da pravokotniki postanejo kvadrati in tako dobimo primer enoličnega poliedra: vsa njegova lica so regularni poliedri in vsi njegovi so vrhovi so obkroženi z enakimi.
V primeru, ko je n=4 je prizma kocka, ki ni samo enolična ampak regularna: lica so vsa enaka, prav tako vrhovi in tudi robovi so enaki.
Fraza »vsa enaka« je narejena z natančnostjo, kot pomoč v teoriji grup. S tem mislimo, da obstaja simetrična operacija, ki transformira katerokoli lice, rob ali vrh v katerokoli drugo lice, rob ali vrh.
Višina n-strane piramide je včasih regulirana, da enakokraki trikotniki postanejo enakostranični. Dejstvo je, da to lahko naredimo samo v primeru, ko jen<6; toda šest enakostraničnih trikotnikov zlije ploskev v ravnino namesto formiranja kota telesa. Trikotna piramida se imenuje tetraeder. Če so tri in tako vsa štiri lica enakostranična je tetraeder regularen.
Z rahlim popačenjem n-strane prizme dobimo n-strano antiprizmo (ali prizmotoid, ali prizmoid), ki ima lica iz regularnih n-poligonov povezanih z 2n enakostraničnim trikotniki.
Višina take antiprizme je narejena tako, da enakostranični trikotniki postanejo enakokraki in tako imamo enoličen polieder s tremi trikotniki in n-poligonov v vsakem vrhu. Ko je n=3, je antiprizma pravilen oktaeder.
Ko je n=5 jo lahko kombiniramo z dvema petkotnima pentagonalnima piramidama baziranima ena na drugi za formiranje regularnega ikozaedra. Par kock z obliko ikozaedra iz Ptolomejeve dinastije si lahko ogledamo v Egiptovski sobi Britanskega muzeja v Londonu.
Sedaj bomo konstruirali štiri izmed petih konveksnih regularnih poliedrov, ki jih je opazoval Platon kot simbol za štiri elemente: zemljo, ogenj zrak in vodo. Različnost med temi štirimi elementi in petimi telesi ni prineslo zmede v Platonovo shemo. Peto telo je Platon opisal kot obliko, ki obdaja cel svet.
Pozneje so srednjeveški alkimisti podali pravo vsebino. Model tega regularnega dodekaedra je bil narejen z lepljenjem skupaj dveh »žog«, vsaka od teh je sestavljena iz petkovnikov obdanih s petimi drugimi petkotniki. Dve žogi sta dejansko zlepljeni skupaj, ker trije robovi formirajo nesimetričen desetkotnik, kakor je formiran z lateralnimi robovi petkotne antiprizme (z enakostraničnimi lateralnimi lici). Steinhaus je lepo opisal zelo lepo metodo za gradnjo takega modela.
Iz kosa lepenke izrežemo mrežo kot je figura, da robovi postanejo prepogljivi,
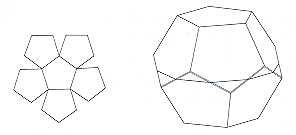
za vsako od krogel. Potem potujmo s topim nožem vzdolž petih strani centralnega petkotnika, da jih postanejo prepogljivi robovi. Namestimo mreži križno drugo na drugo, z zunaj zarezanimi robovi. Povežimo z elastičnim trakom izmenjaje spodaj in zgoraj kote dvojne zvezde, držeč model ploskve z eno roko. Potem roko odmikamo tako, da dopuščamo da se centralni petkotniki pomikajo proč drug od drugega. Vidimo, da dodekaeder raste kot perfekten model.
Spodaj so zbrane najbolj elementarne lastnosti petih Platonovih teles.
PET PLATONOVIH TELES
| IME |
|
SCHLÄFLI-JEV SIMBOL |
|
V |
|
E |
|
F |
|
DIEDERSKI KOT |
| |
| TETRAEDER |
|
{3, 3} |
|
4 |
|
6 |
|
4 |
|
70°32´- |
| |
| KOCKA |
|
{4, 3} |
|
8 |
|
12 |
|
6 |
|
90° |
| |
| OKTAEDER |
|
{3, 4} |
|
6 |
|
12 |
|
8 |
|
109°28´+ |
| |
| DODEKAEDER |
|
{5, 3} |
|
20 |
|
30 |
|
12 |
|
116°34´- |
| |
| IKOZAEDER |
|
{3, 5} |
|
12 |
|
30 |
|
20 |
|
138°11´+ |
Vsak polieder je karakteriziran s Schläfli-jevim simbolom {p, q}, kar pomeni, da ima iz p-stranih poligonov in v vsakem vrhu jih je q. Z V, E in F označimo število vrhov, robov in lic. V vsakem primeru jih je lahko prešteti, toda njihov smisel postane nazornejši, ko jih izrazimo kot funkcijo p-ja in q-ja.
Spodnja gibljiva slika nam nazorno prikazuje vseh pet Platonovih teles.
2. OBSTAJA NATANKO PET PLATONOVIH TELES
DOKAZ:
Dokaz lahko najdemo v Evklidovi knjigi: »Elements« (300 pred Kristusom) in temelji na dejstvu, da če se lica q regularnih p-stranih poligonov srečajo v vrhu, potem je vsota q-kotov v q licih manjša od 360°.
To je rigorozno dokazano v »Proposition 21 of Book IX« v knjigi »Elements«, toda intuitivno si lahko predstavljamo kot nekoga, ki reže q robov in splošča kot poliedra.
Kot primer si mislimo: če primemo kocko za oglišče (rob) ob vrhu in tam prerežemo po robovih in sploščimo kot telesa dobimo:
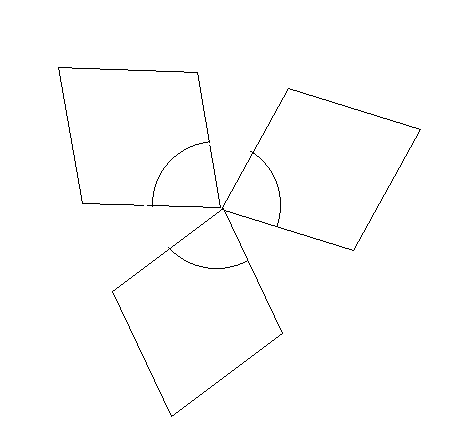Trije pravilni koti imajo še vedno skupen vrh, in vidimo, da je skupna vsota kotov manjša od kompletne revolucije. Tako lahko poligon s p stranicami razdelimo na p-2 trikotnikov, vsota kotov poligon s p stranicami je (p-2) - 180°. Tako je vsak kot regularnega p-stranega poligona je potem enak:
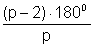
Za regularen polieder, ki ima lica enaka regularnim p-stranim poligonom in q p-stranih poligonov v vsakem vrhu velja
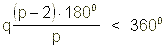
oziroma:
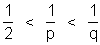
kjer sta p in q najmanj enaka 3 in skupaj ne moreta biti večja od 3.
Tako je možnih samo 5 možnosti za p in q, in vsaka od teh nam da enega od petih možnih regularnih teles:
Če je p = 3 in q = 3, dobimo tetraeder.
Če je p = 3 in q = 4, dobimo oktaeder.
Če je p = 4 in q = 3, dobimo kocko.
Če je p = 3 in q = 5, dobimo ikozaeder.
Če je p = 5 in q = 3, dobimo dodekaeder.
KONEC DOKAZA
Zanimivost:
S Platonovimi telesi so učenci Pitagorejske šole takole predstavili formulo VRENJA:
tetraeder + ikozaeder = 2•Oktaeder + 2•Tetraeder
Vprašanje:
Kako bi to dokazali?
Namig: s pomočjo slik Platonovih teles in števila p-stranih poliedrov (glej tudi tabelo), ki sestavljajo lica le-teh dokaži enakost.
Rešitev:
L (leva stran enačba): tetraeder ima 4 trikotnike; ikozaeder 20 trikotnikov; skupaj jih lahko imata 24.
D (desna stran enačbe): oktaeder ima 8 trikotnikov, ker sta 2, jih imata skupaj 16; tetraeder ima 4 trikotnike, ker sta spet 2, jih imata skupaj 8; skupna vsota je 24 trikotnikov.
Vidimo: Leva in desna stran enačbe sta enaki.
SLIKE IN MODELI
Mojster počasnega govorjenja je bila stara morska jegulja, ki je prihajala enkrat na teden. Učila nas je risanja, raztegovanja ini zgubljanja v špiralah.
Lewis Carroll
Leonardo da Vinci je z dolgimi ozkimi pasovi lesa ustvaril skeletne modele poliedrov. Ko tak model pogledamo v perspektivni legi iz pozicije od zunaj v center nekega lica, to se le-ta pokaže v sliki velikega poligona z ostalimi lici, ki izpolnjujejo njegovo notranjost. Tako risanje telesa se imenuje: Schleglov diagram.
Slike nam prikazujejo vsakega od Platonovih teles v treh aspektih: v običajnem perspektivnem pogledu, mreža, ki je narejena v tabeliranem modelu in Schleglov diagram. Vsakega teh se lahko preveri z opazovanjem narave lic in z urejenostjo oziroma razporeditvijo lic v vrhovih. Očitno je, da je Platon uporabil mreže, da je naredil model teh poliedrov.
REGULARNO TLAKOVANJE
Matematičen vzorec, kot vzorec kakega slikarja, poeta, je lahko čudovit; ideje, kot barve ali besede, se lahko zlijejo skupaj v harmonijo. Lepota je prvi test: tu ni permanentnega prostora v svetu za grdo matematiko.
G. H. Hardy
Povsem verjetno je bil Kepler (1571-1630) prvi, ki je odkril, da so možne poti za zapolnitev ravnine z enakimi regularnimi poligoni. Mi jih bomo poiskali z ustrezno uporabo Schlaffli-jevega simbola {p, q} za tlakovanje z regularnim p-stranimi poligoni, ki imajo vsak vrh obdan s q poligoni.
Primeri: {6, 3,}, {4, 4}, {3, 6} so ilustrirani na sliki
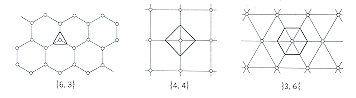
kjer je v vsakem primeru poligon narisan z močnejšo črto je lik ob vrhu:
q-strani poligon, čigar vrhovi so sredinske točke q robov v vrhovih.
(Tlakovanje je ponekod analogno poliedrom, kajti povsem naravno je, da uporabimo besedo rob za skupne robove sosednih poligonov in lica kar za poligon sam.)
Za formalno definicijo moramo povedati, da je tlakovanje regularno, če so regularna lica in če so regularne liku ob vrhovih v vsakem vrhu.
Tlakovanje {6, 3} je pogosto uporabljeno za polaganje keramičnih ploščic npr. v kopalnicah. Vidimo ga tudi lahko v čebeljem panju.
{4, 4} je poznan v obliki kvadratnega lista papirja in v terminu kartezičnega koordinatnega sistema, so njegovi vrhovi kar točke, katerih x in y sta obakrat celi števili. Dual k {p, q} je tlakovanje, katerega robovi so pravokotni na simetrale robov tlakovanega {p, q}.
Tako je dual k {p, q} {q, p}. Druga možnost razlage: vrhovi prvega so centri lic drugega.
{3, 6} je dualen k {6, 3} v sledečem smislu.
V splošnem dual k {4, 4} je enak {4, 4}.
Dejansko je možno pokritje sfere trikrat, z uporabo dvajsetih petkotnikov, ki imajo stranice enke loku velikega kroga.
