lakotos

   Fakulteta za matematiko in fiziko
   Oddelek za matematiko
   Jadranska 19
   1000 Ljubljana

Z DVOMOM DO GOTOVOSTI
(PO LAKATOSU)

VALENTINA LOČNIŠKAR
študentka 4. letnika Oddelka za matematiko

mentor: prof. dr. Damjan Kobal

VSEBINA:

1. OD GOTOVOSTI DO ZMOTNOSTI

1. 1. PLATONIZEM, FORMALIZEM, KONSTRUKTIVIZEM
a. PLATONIZEM
b. FORMALIZEM
c. KONSTRUKTIVIZEM

1. 2. FILOZOFSKA ZAOBLJUBA DELUJOČEGA MATEMATIKA

2. USTVARJANJE NOVE MATEMATIKE

2. 1. LAKATOS IN FILOZOFIJA NEGOTOVOSTI, DVOMA

I. DEJANJE

II. DEJANJE

III. DEJANJE

POVEZAVE

1. OD GOTOVOSTI DO ZMOTNOSTI

1. 1. PLATONIZEM, FORMALIZEM, KONSTRUKTIVIZEM

Če se ukvarjaš z matematiko vsak dan, se ti zdi povsem naravna stvar na svetu. Če pa prenehaš misliti kaj delaš in kaj nekaj pomeni, zgleda kot nekaj najbolj misterioznega. Vprašamo se ali smo sposobni govoriti o stvareh, ki jih še nihče ni videl in jih razumeti bolje kot pa vsakodnevne stvari v življenju. Pojavljajo se tudi vprašanja zakaj je Evklidska geometrija še kar živa, medtem ko je Aristotelova fizika že davno mrtva. Kaj vemo o matematiki in kako to vemo?
Tri standardne dogme nam povejo nekaj o fundamentih matematike:
PLATONIZEM, FORMALIZEM, KONSTRUKTIVIZEM.

a. PLATONIZEM

Pravi, da je matematični objekt realen. Njegov obstoj je neko objektivno dejstvo, neodvisno od tega kaj mi vemo o njem oziroma kakšno je naše znanje o njem. Neskončne množice, števno neskončne množice, neskončno dimenzionalne mnogoterosti, vsi elementi matematičnega sveta so definirani objekti z definiranimi lastnostmi, nekaterimi znanimi, drugimi neznanimi. Ti objekti jasno niso fizikalni ali materialni, eksistirajo zunaj sveta in časa. So stanovitni, ne nastajajo in se ne bodo nikoli spremenili ali izginili. Glede na Platonizem je matematik empiričen znanstvenik, kot nekak geolog. Izumil ne bo prav ničesar, zato ker je tukaj že od nekdaj. Kar dela je v bistvu že vse odkrito.

b. FORMALIZEM

Ta dogma pa pravi, da po drugi strani ni matematičnih objektov. Matematika obstaja na aksiomih, definicijah in izrekih, z drugimi besedami na formulah. V ekstremnem pogledu, obstajajo pravila, po katerih ena formula izhaja iz druge. Formalist ve, da so matematične formule včasih položene v fizikalne probleme. Ko formula podaja fizikalno interpretacijo pridobi pomen, ki pa je lahko napačen ali pa pravi. Toda ta napačnost je povezana s partikularno fizikalno interpretacijo. Čista matematična formula nima pomena in prave vrednosti. Primer, ki demonstrira razliko med formalistom in Platonistom pride iz Cantorjeve hipoteze neskončnosti. Cantor pravi, da ni neskončnega kardilnalnega števila večjega od χ _o (kardinalnost celih števil) in manjšega od C (kardinalnost realnih števil). Kaj bi to pomenilo po Platonizmu? Platonist meni, da so naši aksiomi nepopolni za opis množice realnih števil. Niso dovolj močni, da bi nam povedali vso resnico. Tako je hipoteza o neskončnosti pravilna ali pa ne, kajti ne razumemo množice realnih števil dovolj dobro, da bi našli odgovor. Formalist pa pravi, da je Platonistova interpretacija nesmiselna, saj ni nobenega drugega sistema razen tistega, ki ga mi izberemo, tako da povemo aksiome, ki ga opišejo. Normalno je, da imamo proste roke pri zamenjavi teh aksiomov, če pač želimo to. Do zamenjave pride lahko zaradi pripravnosti ali uporabnosti, morebiti zaradi kakšnega drugega kriterija, ki ga vpeljemo. Ni važno zaradi boljše korespondence z realnostjo, ker tu ni nobene realnosti.
Vidimo, da sta formalist in Platonist na nasprostnih bregovih vprašanja eksistence in realnosti, vendar pa se ne prepirata o principih ali vzroku, ki bi lahko bil dopuščen v matematični praksi.

c. KONSTRUKTIVIZEM

Konstruktivist stoji nasproti obema dvema. Konstruktivist pravi, da je genialna matematika samo tista, ki obstaja na končni konstrukciji. Množica realnih števil ali kakršnakoli druga neskončna množica ne more biti določena na ta način. Posledično konstruktivist gleda na Cantorjevo hipotezo kot na nekaj o čemer ni vredno izgubljati besed.

1. 2. FILOZOFSKA ZAOBLJUBA DELUJOČEGA MATEMATIKA

Mnogo pisateljev se strinja, da je tipični delujoči matematik Platonist med tednom in formalist ob nedeljah. To pomeni, da ko se ukvarja z matematiko je prepričan, da dela z objektivno realnostjo, katere lastnosti se trudi, da bi jih determiniral. Toda, ko želi da bi dal tej realnosti filozofski pridih, vidi da bo pravzaprav najlažje, če o tem sploh nič ne razmišlja in temu ne verjame. Če navedem kar besede dveh pomembnih ljudi:
Dieudonne-ja in Cohen-a:
Prvi pravi:
V osnovi verjamemo v realnost matematike, toda ko nas filozofi napadejo s svojimi paradoksi, planemo, da se skrijemo za formalizem in rečemo:
matematika je kombinacija nepomembnih simbolov in privlečemo na dan teorijo množic. Ko nas končno pustijo na miru, se vrnemo v našo matematiko in delamo kar smo vedno delali z občutkom, ki ga ima vsak matematik, ko dela z nečim realnim. Morebiti je ta občutek varljiv, je iluzija, vendar ustrezna. To je Bourbakijev pogled na osnove. (J. A. Dieudonne, 1970, p.145)

Za vsakega povprečnega matematika, ki edino hoče, da je njegovo delo točno bazirano, je proseča želja, da se izogne težavam s pomočjo Hilbertovega programa. Tu nekdo gleda matematiko kot formalno igro in je edino le zaskrbljen glede vprašanja konsistentnosti. Realistov (Platonistov) odnos je eden tistih, do katerega matematiki čutijo posebno nagnjenost. Ni samo to, da postanejo dovzetni za težave v teoriji množic, ampak se tudi trudijo, da nanje odgovorijo. Če pa jih te težave zelo razburijo, se skrijejo v zavetje formalizma, medtem ko pa je njihov normalni položaj nekje vmes, med Platonizmom in formalizmov. Jasno pa je, da se trudijo uživati najboljšega izmed obeh.
(P. J. Cohen, "Axiomatic Set Theory", ed. D. Scott)

V teh vprašanjih od Dieudonneja-ja in Cohen-a smo uporabili termin "formalizma" v smislu filozofskega odnosa, ki je pa v čisti matematiki nepomembna igra. Bilo bi potrebno, da zavrnemo formalizem kot filozofijo matematike, ki pa na noben način ne sme vsebovati kritiko matematične logike. Nasprotno pa so logiki, katerih edina matematična aktivnost je študij formalnih sistemov, v najboljšem položaju, da upoštevajo nenormalno razliko med matematiko tako kakršna je in med matematiko, ki je shematizirana v notaciji formalnega matematičnega sistema.

2. USTVARJANJE NOVE MATEMATIKE

V dokazih in spodbijanjih je Imre Lakatos predstavil sliko logičnega matematičnega raziskovanja. Za boljšo predstavo si najprej oglejmo s čim se je ukvarjal Imre Lakatos.

2. 1. LAKATOS IN FILOZOFIJA NEGOTOVOSTI, DVOMA

TEMELJITEV (kot postavljanje temeljev) oz. v originalu FOUNDATIONISM, so t. i. poskusi, da bi zgradili (dognali) bazo za matematično gotovost, je prevladovalo v filozofiji matematike v 20. stoletju. Radikalno različna alternativa je prišla s prepoznavno z značilnim delom Imre Lakatosa. Iskanje temeljev je v znanosti vodilo v tradicionalni problem induktivne logike: kako izpeljati glavne zakone iz partikularnih eksperimentov in raziskav. V l. 1934 se je zgodila revolucija. Karl Popper je predlagal, da je bolj kot potrebno, zadostno, da se dokaže zakone znanosti z induktivnim dokazovanjem. Popper je dejal, da znanstvene teorije niso izpeljane iz dejstev. Raje so rezultati hipotez, špekulacij, ugibanj in so opredmetene kot eksperimentalni testi. Imre Lakatos je uporabil svojo epistomološko analizo za formalizacijo matematike, toda za neformalno matematiko, matematiko v procesu razvoja, tako matematiko kakršno poznajo matematiki in študenti matematike. Formalizirano matematiko, ki se ji je filozofija posvetila v prejšnjem obdobju, jo je bilo v bistvu sedaj težko najti kjerkoli na Zemlji ali v nebesih, stran od tekstov in zapisov simbolične logike.

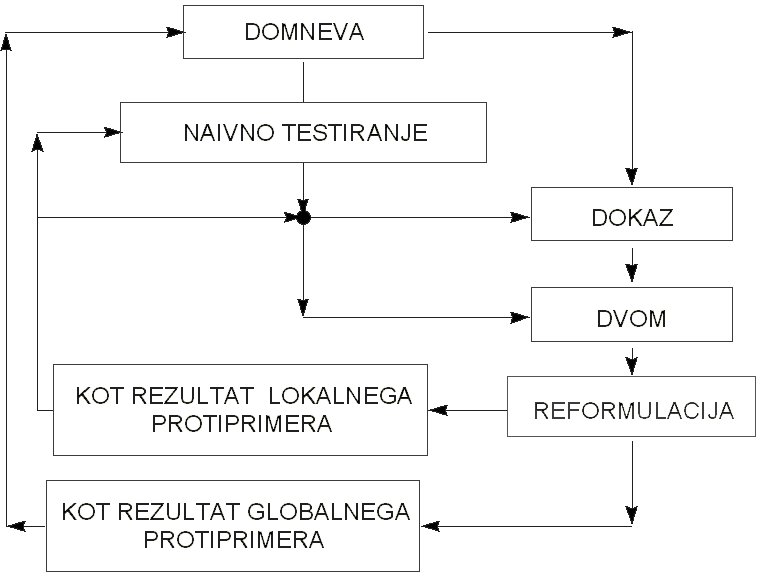
Lakatosovo delo: Proofs and Refutations je zapisano v obliki dialoga, ki poteka v razredu. Učitelj predstavlja tradicionalen dokaz kot Couchy Eulerjevo formulo, v kateri se robovi poliedra razprostirajo in tako formirajo mrežo v ravnini in jo uspešno reducirajo na posamezne trikotnike. Dokaz še ni bil končan, ko je razred že izdeloval menežarijo protiprimerov.

Boj se je začel! Kaj je dokaz pokazal?
Kaj vemo iz matematike in kako bi to pokazali?
Diskusija je tekla globlje in globlje in prehajala na raven popačenega sklepanja, tako matematičnega kot logičnega. Vemo pa, da vedno obstaja več različnih možnosti pogleda na sam kontekst. V tako različnih točkah dialektičnega ognja so pripombe privedle do genialne dokumentirane zgodovine dokaza kompleksnosti.

Glavni tekst je v delu racionalne konstrukcije dejanske zgodovine ali bolje rečeno, kakor je naredil Lakatos, da je dejanska zgodovina parodija na njegovo racionalno rekonstrukcijo problema.

Sedaj se pa vrnimo na idejo razčlenitve dokaza Euler- Descartesove formule. Učitelj je njegov razred so študirali znano Euler-Descartesovo formulo za polieder : V - E + F = 2, kjer je V - število vrhov, E število njegovih robov in F število njegovih lic.

Za ilustracijo si v tabeli lahko ogledamo vrednosti za V, E in F znanih poliedrov.

	V	E	F
TETRAEDER	4	6	4
EGIPČANSKA PIRAMIDA	5	8	5
KOCKA	8	12	6
OKTAEDER	6	12	8

Učitelj predstavi tradicionalen dokaz v katerem je polieder razpet v ravnini. Ta dokaz je takoj sledil z "zajezitvijo" protiprimerov, ki so jih predstavili študenti. Pod vplivom protiprimerov je bila oblikovana trditev in dokaz je bil pravilen in elaboriran. Novi protiprimeri so narejeni, prav tako tudi nove sodbe. Ta razvoj je predstavil Lakatos kot model za razvoj matematičnega znanja v splošnem. Lakatosov hevristični primer za dokaze in spodbijanja, ki je bil formuliran za matematično kulturo v širšem smislu je bil jasno uporabljen. Uporabili so ga posamezniki v svojih prizadevanjih za oblikovanje nove matematike.

Avtor je uporabil to metodo s skromnim uspehom v svojih razredih. Začetni udarec je, ko predstavimo (poslušalcem) študentom ne fiksen problem, ki je potem razbit, ampak odprto končno situacijo možnostnega odkrivanja, lahko in mora biti potencialno premagan. Boljši študenti so v takem načinu doživeli občutek veselosti in svobode. Ilustrirala bom to metodo s primerom iz elementarne metode števil.

Začetno trditev bomo imenovali seme. Ta trditev bo ena izmed zanimivih in dokaj lahkih. Objekt vaje je, da mora študent zalivati seme, da ta raste in se razvije v čvrsto rastlino. V bistvu bomo videli, da razred vedno lahko obdarimo z različnimi semeni in jih izberemo za zalivanje, odvisno od vaje.

I. DEJANJE
Seme:	Če se število konča z 2, je deljivo z 2.

Primer:	42 se konča z 2 in je deljivo z 2.

Dokaz:	Število je sodo, če se konča z 0, 2, 4, 6, 8. Vsa soda števila so deljiva z 2. V posebnem tista, ki se končajo z 2, so deljiva z 2.

Dokaz:	(nekoliko izumetničen) Če je število, zapisano s števkami: ab ... c2, potem je jasno, da je oblike: (ab ...co) + 2, zato je oblike: 10Q + 2 = 2(5Q + 1).

Idejni preskok:	Če se število konča z N, potem je deljivo z N.

Komentar:	Bodimo drzni, ko delamo objektivne posplošitve. Nebesa se ne bodo podrla, če se bo izkazalo, da je napačno.

Primer:	Če se število konča s 5, potem je deljivo s 5. To so na primer števila: 15, 25, 12805, itd..

Protiprimer:	Če se število konča s 4? Ali je potem deljivo s ?. Ali je 14 deljivo s 4? Ni!

Ugovor:	Nekatera števila se končajo s 4 in so deljiva s 4. Npr.: 24 Nekatera števila se končajo z 9 in so deljiva z 9. Npr.: 99

Povzetek ugotovitev:	Za števila 1, 2, ...,9 lahko rečemo, da jih lahko razdelimo v dve kategoriji: Kategorija I: Take števke N, da se vsaj eno število konča z N in je deljivo z N. Kategorija II: Take števke N, da so števila, ki se končajo z N deljiva z N samo včasih.

	Kategorija I: 1, 2, 5
	Kategorija II: 3, 4, 6, 7, 8, 9

Postavitev stvari na pravo mesto:	Kaj je s števili, ki se končajo z 0? Ali so deljiva z 0? Ne. Toda deljiva so z 10. Pa poglejmo kako je s takim primerom. Jasno je, da ta pojav ni primeren za seme.

Definicija:	Imenujmo ta števila iz kategorije I. magična števila. Ta števila imajo očarljivo lastnost.

Poskusna trditev:	Števila 1, 2, in 5 so magična števila. To so edina magična števila.

Protiprimer:	Kaj pa število 25? Ali ni magično? Če se število konča s 25, je deljivo s 25. Npr. 25 ali 625.

Ugovor:	Mislili smo, da govorimo o samostojnih števkah.
Spodbitje:	Dobro, bili smo iznadljivi. Vendar 25 je fenomen, ki nas vseeno zanima. Odprimo o njem posebno preiskavo!

Izboljšava:	Naj sedaj N predstavlja ne nujno samostojno števko, ampak celo skupino števil, kot so 23, 41, 505 itd. Naredimo definicijo, da je N magično število, če je število, ki se konča z N, deljivo z N. Ali ima tako napravljena definicija sploh smisel?

Primer:	Ima. 25 je magično, 10 je magično, 20 je magično, 30 je prav tako magično število.

Protiprimer:	30 ni magično. 130 ni deljiva s 30. Pomislimo sedaj, ko vemo, da je 25 magično.

Trditev:	25 je magično število.

Dokaz:	Če se število konča s 25, potem je njegova oblika v števkah: abc... e 25 = (abc ... e00) + 25, tako je oblike: 100. Q + 25 = 25.(4.Q + 1)

Izboljšava cilja:	Poiščemo čudežna števila.

Zbirka ugotovitev:	1, 2, 5, 10, 25, 50, 100, 250, 500, 1000 so vsa magična števila.

Opazovanje:	Ali so ta magična števila, ki jih imamo lahko produkt 2 in 5? Dejansko nekatera so.

Domneva:	Neko število N oblike: N = 2^p . 5^q, kjer p ≥ 0, q ≥ 0 je magično št.

Komentar:	Izgleda upravičeno. Kaj bi lahko izgubili?

Protiprimer:	Vzemimo: p=3, q=1. Potem je N = 2³. 5 = 40. Ali je število, ki se konča s 40 vedno deljivo s 40? Ni. Npr.: 140.

Izboljšava:	Kakšna je drugačne pot okoli našega razmišljanja? Vsa magična števila, ki smo jih našli so oblike 2^p. 5^q.

Opazovanje:	Morebiti so vsa magična števila te oblike. Ali ni to ravno to kar smo predpostavili?

Spodbitje:	Ne, kar smo mi predpostavili je drugačna pot. Število 2^p. 5^q je magično. Ali vidimo razliko?

Trditev:	Če je N magično, potem je oblike: 2^p. 5^q

Dokaz:	Vzemimo število, ki se konča z N. (opozorilo: v tej izjavi je N vzeto iz množice številk) Potem število izgleda: abc ...eN, na eniški način: Radi bi ga razcepili kot prej. N naj ima d(N) številk. Potem je število abc ... eN res oblike: abc ...e00... + N, kjer je d(N) število ničel na koncu. Zaradi tega je število oblike: Q.10^d(N) + N Če pogledamo za: d(N) = 2, potem: abc... e00 + N = Q.10² + N Vsa števila, ki se končajo z N so te oblike. Obratno, če je Q kakršnokoli število, se število Q.10^d(N) + N konča z N. Če je N magično število vedno deli Q.10^d(N) + N. Če pa N deli N, potem N deli tudi Q.10^d(N) + N za vsak Q. Toda Q je lahko enostavno število 1. Potemtakem N deli 10^d(N). In kjer je: 10^d(N) = 2^d(N) . 5^d(N) primarna faktorizacija, sledi, da je N lahko samo 2 ali 5.

Običajna domneva:	Sedaj vemo, da je magično število oblike N = 2^p . 5 ^q za celi števili p, q ≥ 0. Sedaj pa bi radi vse obrnili nazaj. Tako bi dobili zadosten in potreben pogoj za magičnost.

Nov pogled na ugotovitve:	Odkar vemo, da so vsa magična števila oblike: N = 2 ^p . 5 ^q, se pojavi problem: kaj mora veljati za p in q, da je rezultat magičen?

Domneva:	p = q.

Ugovor:	Potem je N = 2^p . 5^q = 10^p ali 1, 10, 100... Toda tu so tudi druga magična števila.

Domneva:	p ≥ q?

Protiprimer:	p = 3, q = 1, N = 2³ . 5¹ = 40. To ni magično.

Opazovanje:	V tem delu je torej nekaj zelo subtilnega, nežnega. To zagrne zaveso na I. dejanje. Proces gre naprej za tiste z ustreznimi interesi in načini.
II. DEJANJE V tem delu je hevristična meja individualno skrajšana v obširnem pisanju.
Strategija posvetovanja:	Vrnimo se nazaj na dokaz potrebnosti oblike: N = 2^p . 5 ^q Videli smo, da če je N magično število, potem je deljivo z 10^d(N). Spomnimo se, da d(N) sestoji iz števil iz mn. št. N. Morda je tudi to potrebno! Mogoče bo tu preboj bojne črte!

Trditev:	N je magično število, če in samo če deli 10^d(N).

Dokaz:	Potrebnost je že bila dokazana. Če se N konča z N, potem vemo, da je oblike Q.1 ^d(N) + N. Toda N deli N in N prav tako mora deliti 10 ^d(N). Potemtakem mora deliti Q.10^d(N)

Estetični ugovor:	Če je to res, potem vemo, da je potreben in zadosten pogoj za magičnost to število N, ki pa ni faktorizirano na obliko 2 ^p . 5 ^q.

Posvetovanje:	Kdaj N = 2^p . 5^q deli 10^d(N)? Dobro: 10^d(N) = 2^d(N). 5^d(N), potem je nujno potreben in zadosten pogoj za to: p ≤ d(N), q ≤ d(N) Potem je ekvivalentno: max(p,q) ≤ d(N). Še kar imamo porušen d(N) s katerim se borimo. Tega pa nočemo. Radi bi pogoj za N, ali če je možno za p ali q. Kako bi preoblikovali max (p,q) ≤ d(N) = d(2^p . 5^q) v bolj uporabno obliko? Kakor vemo: za p = q potem trditev velja. Poglejmo stanje zapisano v novi obliki: p = max (p,p) ≤ d(2^p. 5^p) = d (10^p) Sedaj je število številk v 10 ^p p+1 To je: p≤ p+1, kar je vredu kakor je če v splošnem damo ven potenci števil 2 in 5. Napisano: Q = p + h, kjer je h>0.

Ugovor:	Kaj če p>q? Potem je p+h=q, kar je nemogoče s h>0.

Ovržba:	Obravnavajmo kasneje.

Posvetovanje:	max (p, p+h) ≤d(2^p. 5^p+h) = = d(2^p . 5^p . 5^h) = d(10^p . 5^h) Naj bo sedaj h>0, max (p, p+h) = p + h. Tako je število števk v 10^p. Q, kjer je Q število enako p+ število številk v Q. Potemtakem je p+ h ≤ p + d(5^h) ali h ≤ d(5^h).

Dvomi:	Kdaj je potem res, da h > 0 in h ≤ d(5^h)?

Poskušanje:	h=1:	1 ≤ d(5¹)
	h=2:	2 ≤ d(5²)
	h=3:	3 ≤ d(5³)
	h=4:	4 ≤ d(5⁴)
	h=5:	5 ≤ d(5⁵) = d(3125) = 4

Ugovor:	h ≤ d(5ⁿ), če in samo če je h = 1, 2, 3,.

Dokaz:	Izpuščen.

Repriza:	Kaj pa p > q?

Posvetovanje:	Naj bo p = q + h, h > 0. q+h = max (q + h, p) h ≤ d(2 ^q+h, 5^q) = 10 (10^q. 2^h) = q + d (2^h), ali h ≤ d(2^h). Kdaj je h ≤ d(2^h)?

Poskušanje:	h = 1:	1 ≤ d(2¹)	O.K.

	h = 2:	2 ≤ d(2²)	No vredu.

Domneva:	h ≤ d(2 ^h) če in samo če h = 1.

Dokaz:	Izpuščen.

Trditev:	N je magično število.

Dokaz:	Izpuščen. Zaradi pričakovanja nadaljnega razvoja, bi radi to trditev zapisali v drugačni obliki.
Trditev:	N je magično število če in samo če N = 2^p . 5^q, kjer 0 ≤ q - p+1 ≤4

Dokaz:	Izpuščen.

III. DEJANJE

bi se mogoče lahko pričelo z vprašanjem, kaj bi se zgodilo, če bi naša števila zapisali v drugačni bazi in ne v desetiški. Kaj pa osnovni bazi, ali pa bazi enaki produktu osnovnih?

POENOSTAVLJEN LAKATASOV MODEL
ZA HEVRISTIKO MATEMATČNEGA ODKRIVANJA

POVEZAVE:

O Lakatosu, si lahko še pogledate na straneh interneta:

Imre Lakatos

POPPER, KUHN, LAKATOS AND AIM-ORIENTED EMPIRICISM

Lakatos's Methodology of Scientific Research Programs

Lakatos - an Introduction; A Contribution to the Theory of Science