
Stvaritve, ki so jih dosegli z uporabo egipčanske matematike, se lahko primerjajo s katerimkoli sodobnim dosežkom in so še danes spomeniki, ki še vedno begajo človeštvo. Velika piramida v Gizi je edina ohranjena izmed sedmih čudes antičnega sveta. Dokončali so jo pred 4500 leti, da bi ohranila telo faraona Keopsa (ali Kufuja), in je obenem spomenik matematičnemu znanju starodavnih Egipčanov.
Osnovna ploskev je skorajda popoln kvadrat s stranicami, katerih dolžina odstopa od 230,4 m za manj kot 0,05%. Prvotna višina 146,7 m je bila dolžina polmera kroga, katerega obseg je bil enak obsegu osnovne ploskve piramide. Stranske ploskve so enakostranični trikotniki, obrnjeni skoraj točno proti severu, jugu, vzhodu in zahodu. Dva jaška, ki vodita iz celice, ki je nekoč vsebovala Keopsov grob, sta usmerjena proti zvezdi Alfa v Zmajevem ozvezdju in proti Orionovemu ozvezdju.
Nesporno vemo, da je babilonska geometrija vsebovala mnogo zaključkov, o katerih nimamo ohranjenega nobenega dokumenta iz egipčanskih virov; toda arhitekturne in namakalne mojstrovine civilizacije ob Nilu nam vsiljujejo domnevo, da je morala imeti ta civilizacija izdelan sistem natančnih pravil za merjenje. Še več - dve dokumentirano dokazani dejstvi kažeta, da je Egipt v tem prekosil Mezopotamijo. Egipčanska vrednost za razmerje (π) med obsegom kroga in njegovim premerom je, kot navaja Ahmesov papirus, 3,16, kar je dosti bliže resnični vrednosti (3,14159...) od babilonske (in biblijske) vrednosti 3,0. Egipčanska formula za prostornino piramide, kot jo navaja moskovski papirus, je pravilna, babilonska pa ne.
Egipčanski pravili za ploščino (A) in obseg (P) kroga, izraženi s premerom (d=2r), sta:
A = (8d/9)2 =
(256/81).r22 prib. πr2
P = (8/9)2 . 4d = 2 (256/81).r prib. 2πr
Iz tega sledi, da je π pribl. 3,1605. Nič gotovega ne vemo o tem, kako so geometri v svetiščih prišli do te številke. Možna je razlaga, da to število predstavlja srednjo vrednost med polovičnima obsegoma dveh enakostraničnih dvanajsterokotnikov, od katerih je eden včrtan, drugi pa očrtan krogu s polemrom 1; ali - kar pripelje do enakega rezultata - da je to srednja vrednost ploščin včrtanega 12-straničnega in očrtanega 6-straničnega pravilnega mnogokotnika. Ustrezajoči števili sta 3,1058 in 3,2
154, tako da je njuna srednja vrednost 3,1601.
Če pogledamo situacijo s stališča nujne potrebe po sistemu merjenja, lahko - če pustimo ob strani razvijanje astronomije zaradi izpopolnjevanja koledarja in zaradi lažjega vzdrževanja oblasti nad suženjskim ljudstvom, ki se je vraževerno balo nenavadnih nebesnih pojavov, kot je npr. mrk - razvrstimo glavna vprašanja v tri skupine:
a) merjenje zemljišča (odtod ima geometrija tudi ime);
b) arhitektura, zlasti gradnja spomenikov, povezanih s koledarjem;
c) količinske mere za dajatve ali trgovino.
Kar zadeva merjenje, dolgujemo verjetno Egiptu prav toliko kot Mezopotamiji, ker so tempeljski merilci ugotovili:
a) razmerja med kvadrati in pravokotniki; te so Babilonci in njihovi grški učenci uporabljali kot racionalno osnovo za reševanje problemov, ki bi jih mi izrazili kot kvadratne enačbe;
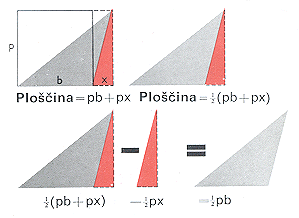
b) dejstvo, da je ploščina trikotnika enaka polovični ploščini pravokotnika z enako višino in enako osnovnico;
c) da lahko dobimo bolj ali manj natančno ploščino kroga, če pomnožimo kvadrat premera z nekim določenim številom.
Nedokumentirani dokazi, ki pa nam jih arhitektura naravnost vsiljuje, so v tesni zvezi z zahtevami koledarske astronomije. Da bi določili poldnevnik in potem tudi sezidali piramido, ki je imela stranice obrnjene proti severu, jugu, vzhodu in zahodu tako natančno, kot so stranice Velike piramide v Gizi, so morali znati razpoloviti kot med položajema vzhajajočega in zahajajočega sonca ob enakonočjih ali pa dobiti natančno smer najkrajše sence, ki jo meče sonce opoldne, s tem, da so razpolovili kot med njenima položajema ob enaki dolžini dopoldne in popoldne. Zato lahko sklepamo, da so egipčanski "natezalci vrvi", kakor so merilce in arhitekte iz svetišč imenovali njihovi grški učenci, znali razpoloviti kot - verjetno s klinom in vrvjo za risanje krogov in ravnih črt v pesek. Precej verjetno je tudi, da so izkušnje z nihanjem grezila tik nad vodoravno ravnino potrdile njihovo domnevo, ki so jo skoraj gotovo že uporabljali v astronomskih računanjih - namreč domnevo, da je daljica, ki povezuje središče kroga s stičiščem krožnega oboda in tangente, na to tangento pravokotna.
Maksimalna napaka pri stranicah in kotih Velike piramide je majhen del od 1%. Zato je popolnoma očitno, da so znali arhitekti in zemljemerci z dokajšnjo natančnostjo načrtati pravi kot. Enako verjetno je, da so se pri postopku z vrvjo in klinom naslanjali na enega od teh treh načinov:
1. uporaba Evklidove konstrukcije, ki je tudi način za razpolavljanje daljic;
2. izkoriščanje dejstva, da dobimo iz vrvi z vozli na razdaljah 5 : 4 : 3, če jo ob vozlih pritrdimo na tla, pravokoten trikotnik;
3. okoriščanje z dejstvom, da je kot, ki združuje obe krajišči premera kroga s katerokoli točko na krožnici, pravi kot.
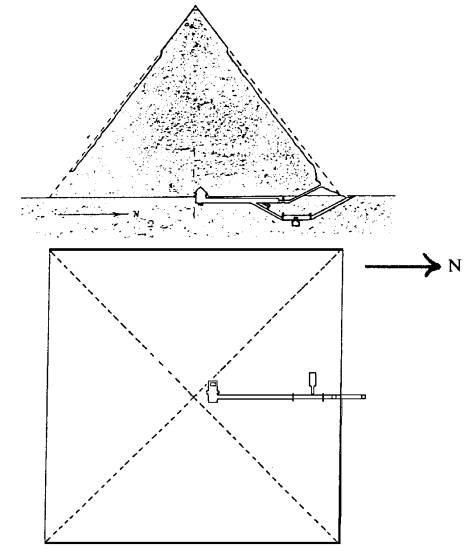
Stranice piramide v Gizi so obrnjene natanko proti severu, jugu, vzhodu in zahodu. Spodnja skica prikazuje dve geometrijski konstrukciji; verjetno so uporabili eno izmed njiju, da so dobili omenjeni rezultat.
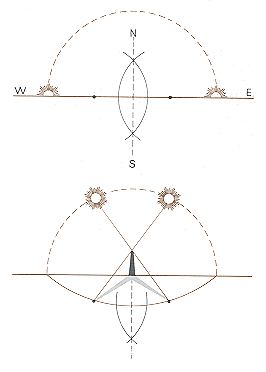
1. razpolovi črto, ki povezuje točki, v katerih sonce vzhaja in zahaja ob enakonočju.
2. Poišči položaj, v katerem je opoldanska senca najkrajša, tako da razpoloviš kot med položajema, ki ju zavzemata enako dolgi senci dopoldne in popoldne.
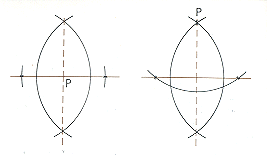
Egipčanski arhitekti so nedvomno že znali potegniti pravokotnico na vodoravno črto v določeni točki p, prav tako so tudi že znali narisati pravokotnico na vodoravno črto iz dane točke.
Glede na vse to je videti zelo verjetno, da so tako Egipčani kot Babilonci poznali prvi način in da so Egipčani poznali tudi drugega. Za tretji način je dokumentirano dokazano, da so ga Babilonci poznali in da so lahko tudi koristno uporabljali svoje tabele kvadratov, ko so spoznali razmerje 5 : 4 : 3 za poseben primer pravila, ki ga ponazarjajo še drugi numerični primeri (npr. 20 : 16 : 12 in 17 : 15 : 8). Odveč je pri tem omenjati Pitagorov izrek (h2 = p2 + b2), ki pravi, da je kvadrat ob daljši stranici pravokotnega trikotnika enak vsoti kvadratov ob drugi dveh stranicah. Jasno je, da so babilonski geometri poleg najpreprostejšega načina za risanje pravega kota (5 : 4 : 3) dobro poznali še mnogo primerov pitagorejskih razmerij, saj samo ena tabela navaja 15 takšnih skupin s po tremi celimi števili. Poiščemo jih lahko na več preprostih načinov; npr.:
če je
h2 = p2 + b2,
potem je:
b2 = h2 - p2 = (h + p)(h - p)
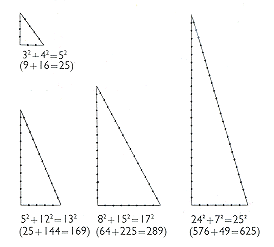
Egipčanski geometri so morali poznati vsaj en primer Pitagorovega izreka, da je kvadrat nad najdaljšo stranico pravokotnega trikotnika enak vsoti kvadratov nad drugima dvema stranicami in sicer primer pravokotnega trikotnika s stranicami, dolgimi 5, 4 in 3 enote. Babilonski matematiki so poznali 15 takih pitagorejskih trojic celih števil, kot so prikazane na skici.
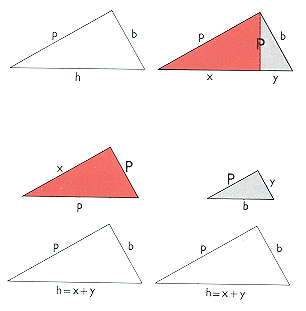
Pravokotnica iz pravega kota na hipotenuzo deli pravokotni trikotnik na dva trikotnika, ki imata oba enake kote kot prvi trikotnik.
V pravokotnem trikotniku, v katerem je najdaljša stranica h, drugi dve pa sta pa p in b, je p2 + b2 = h2.
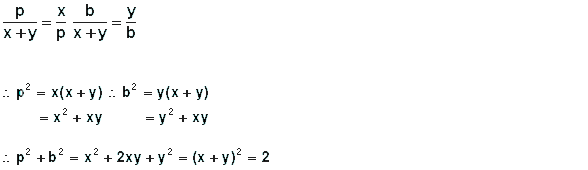
Če sta dve trikotnikovi stranici enaki, sta enaka tudi njima nasprotna kota, in narobe, če sta dva trikotnikova kota enaka, sta enaki tudi ustrezni stranici. Da to dokažemo, v obeh primerih razdelimo trikotnik na dva dela s črto, ki razpolavlja vrhnji kot. V prvem primeru vemo, da je AB = AC. Ker je AD, ki razpolavlja BAC, skupna obema trikotnikoma, imata torej ta dva trikotnika enaki dve stranici in kot med njima. Zato sta identična, torej sta enaka tudi ustrezajoča si kota ACB in ABC. V drugem primeru vemo, da je ABC = ACB. Trikotnika imata, kot je razvidno iz konstrukcije, dva para enakih kotov, kar pomeni glede na 1. zahtevek, da so enaki vsi trije pari. Ob koncih daljice AD imata torej oba trikotnika enaka kota. Zato sta identična in sta enaki tudi ustrezajoči si stranici AB in AC.
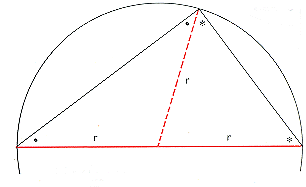
V polkrogu sta črti, ki povezujeta neko točko na obodu s krajiščema premera, pravokotni druga na drugo. Ravna črta iz središča do vrha seka tak trikotnik v dva enakokraka trikotnika, od katerih ima eden enaka kota ° + * + (° + *) = 180° ¤ (° + *) = 90°.
Vsako določanje višine sonca, ki je zasnovano na dolžini sence ali kakšni drugačni uporabi sence pri merjenju višine kake zgradbe, predpostavlja spoznanje:
a) da je rob svetlobnega žarka raven;
b) da so razmerja med ustrezajočimi si stranicami enakokotnih trikotnikov enaka.
Prva predpostavka je v skladu z izkušnjami ljudi, ki so vajeni gledati iskrenje prahu v snopu skozi ozko špranjo prihajajoče svetlobe in je vključena v astronomskih razlagah na najnižji stopnji. Neki ohranjen papirus z opombo k navodilom za zidarje, ki so zidali piramido, pa očitno upravičuje naše mnenje, da so Egipčani poznali tudi drugo postavko in se po njej ravnali. Zatrdno vemo, da so jo upoštevali arhitekti v mezopotamskih svetiščih.
Mere za dajatve in za trgovsko blago spadajo v našo temo v zvezi z odkritjem pravil za določanje prostornine posod. Najpreprostejši primer je prostornina (hb2) četverostranične prizme z višino h in s kvadratno osnovno ploskvijo, ki ima stranico b. Iz tega izhaja tudi prostornina tristranične prizme, izračunane na podlagi pravila za površino trikotnika. Egipčanski odmerjevalci dajatev so poznali veljavno pravilo za prostornino (πr2h) kašče valjaste oblike s polmerom r in višino h. Najbolj je presenetljivo to, da so znali pravilno izračunati tudi volumen odseka piramide, kakor navaja moskovski papirus. Čeprav ne vemo, kako so prišli do tega pravila, lahko s precejšnjo verjetnostjo rekonstruiramo njihov pristop, če si ogledamo preprostejši primer - volumen cele piramide. Vendar bomo odkrito priznali možnost, da se lahko motimo. Kadar se zabavamo z ugibanjem o tem, kako so se ljudje v daljnjih časih dokopali do svojih spoznanj, stojimo na razmeroma trdnih tleh. Če se vprašamo; kako so lahko rešili ta problem s sredstvi, ki so jih zagotovo imeli, sicer pa storimo najbolje, če premislimo, kakšna sredstva so verjetno imeli na voljo.
Do danes ni znano, ali so egipčanski geometri v resnici poznali figurativna števila. Zagoto vemo le to, da so bila trikotniška in piramidna števila dobro znana Babiloncem iz leta 2000 pr. n. š. V 6. stoletju pr. n. š. so z njimi očarali Grke, tako da so gledali nanje z vraževernim oboževanjem. Če so Egipčani kaj vedeli o teh številih, potem si je lahko predstavljati način, kako so najbrž prišli do pravilne prostornine piramide, čeprav ni verjetno, da bi prešli vse stopnje naslednjega dokaza.
Iz figurativne predstavitve piramide, ki je visoka n plasti in katere osnovna ploskev ima n točk dolgo stranico, bi atomist iz 5. stoletja pr. n. š. lahko uganil pravilno formulo za volumen piramide. Izrazil bi jo z njeno višino (h) in z dolžino njene osnovnice (B), torej 1/3 hB2. Moral pa bi znati dovolj dobro operirati z velikimi števili, da bi opazil, kako se relativna napaka v aproksimaciji (2n + 1)(n + 1)n.6-1 ~1/3n3 toliko bolj zmanjšuje, kolikor bolj povečujemo n. Po tem bi se lotil dokazovanja te formule tako, da bi uporabil geometrijsko mišljenje. Demokrit, oče atomizma, se hvali, da je obvladal vse znanje egipčanskih "natezalcev vrvi", in tako priča, kako veliko dolguje grška geometrija svojim prednikom. Sam je na geometrijski način izvedel manjšo adaptacijo egipčanske formule za pravilne piramide na peterokotni, šestorokotni itd. osnovni ploskvi. Vsi ti primeri imajo analogne primere na področju figurativnih števil. Vendar pa je edina geometrija, ki nam je potrebna, če že poznamo figurativne formule za vsote naravnih števil in njihovih kvadratov, daleč za tistim, kar so poznali Egipčani 2000 let pred Demokritom.

Velika piramida je bila tako kot piramida v Sakkari (na sliki) sprva stopničasta, šele pozneje so zidarji stopnice zapolnili in tako zgladili njeno površino. V bistvu je očrtana robovom vrste pravokotnih plošč enake debeline (s) in z enakomerno manjšajočo se osnovnico. Če B - a predstavlja dolžino najnižje plasti, so dolžine plasti neposredno nad njo:
B - 2a, B - 3a, B - 4a itd.
Iz tega lahko ob poznavanju figurativnih števil in geometrije, kakršno so poznali egipčanski merilci, izpeljemo formulo za prostornino piramide.
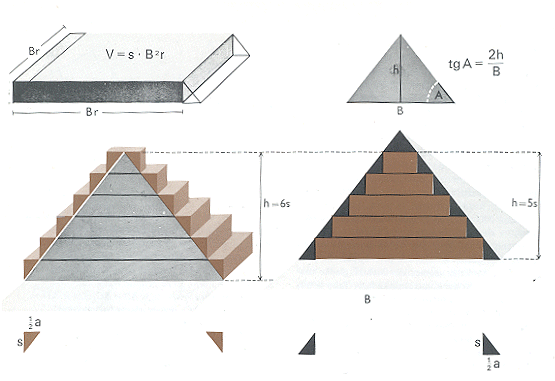
Spomnimo se, da je bila Velika piramida najprej zgrajena stopničasto, tako kot prve egipčanske piramide in kot tolteški spomeniki v Mehiki; gladke stranice so šele iz druge konstrukcijske faze; tako je bila pravzaprav očrtana okrog robov zaporednih kvadratnih plošč enake debeline (s) in s stranicami, katerih dolžina (B) se je enakomerno manjšala (za a). Če si zamislimo piramido, ki bi bila v takšno strukturo včrtana, velja isto pravilo, vsota slojev pa bo za 1 večja. Če ima orisana stopničasta piramida n plasti in je osnovnica (B) prve ploskve enaka osnovnici piramide, so dolžine stranic posameznih plasti takele:
B; B - a; B - 2a; B - 3a ... B - (n - 1)a
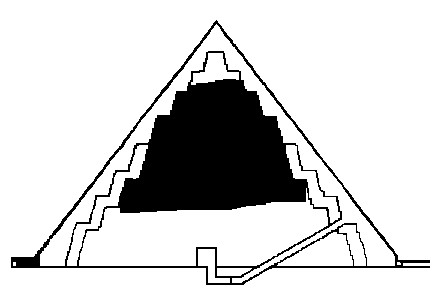
Včrtana stopničasta piramida vključuje sloje s stranicami vseh pravkar navedenih dolžin razen prve.
Površina r-tega sloja je torej (B - ra)2, njegova prostornina pa s (B - ra)2. Če označimo volumen očrtane stopničaste piramide z Vo, volumen včrtane pa z Vv, bo volumen gladke piramide (V) tak, da bo Vo > V > Vv, in bo:
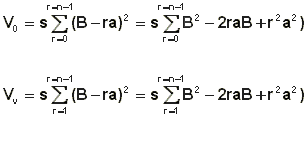
Zato lahko napišemo:
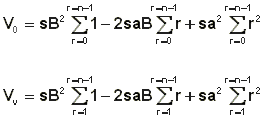
Prvi člen Vo pomeni, da moramo sB2 n-krat sešteti, prvi člen Vv pa pomeni, da moramo sB2 sešteti (n - 1)- krat. Naslednja dva člena ustrezata prvim (n - 1) trikotniškim in prvim (n - 1) piramidnim številom ter sta za Vo in Vv enaka. Tako dobimo:
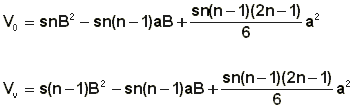
Naša slika kaže, da je sn = h in a = sB : h, tako da je:
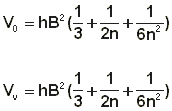
Če je slojev samo deset, lahko torej rečemo, da se izrazi (E) v oklepajih skrčijo na 1/3 + 31/600 in 1/3 - 29/600 ali E π 1/3 *+- 1/20. Za n = 100 je E π 1/3 +- 1/200; za n = 1000 je E π 1/3 1/200 itd. Ko se število slojev bolj in bolj veča, se oba izraza približujeta isti mejni vrednosti, tj. eni tretjini, tako da je:
![]()
Če poznamo formulo (πr2) za ploščino kroga, nas to razmišljanje privede do ustrezne formule (1/3 πr2h) za prostornino stožca. O tem nimamo vse do grške dobe ničesar ohranjenega, vendar pa morda ni brez pomena dejstvo, da je bil prvi Grk, ki je to formulo odkril, ravno Demokrit. Jasno je, da Egipčanom ni treba pripisovati tako podrobne raziskave, kot je naša. Če bi računali prostornine očrtanih in včrtanih stopničastih piramid z vedno manjšimi stopnicami, bi kaj lahko ugotovili, da leži prostornina gladke piramide med mejama, ki se postopno približujeta 1/3 hB2. Celo tako preprosta in zgolj empirična obravnava problema pa napoveduje tisto, kar bi lahko imenovali dvostranska metoda izčrpavanja. Ta je omogočila Arhimedu, da je vklenil π med dve določeni meji:
![]()
Na možnost, da bodo poznejša odkritja postavila egipčansko matematiko na višjo znanstveno raven, kot so ji jo bili doslej pripravljeni priznavati nekateri znanstveniki, kaže neki astronomski tekst, najden v grobnicah 20. dinastije faraonov (okrog 1000 pr. n. š). Neugebauer reproducira odlomek takega teksta iz grobnice Ramzesa VII. Na njem je prikazano, kako se ugotavlja nočni čas skozi vse leto, tako da se višina neke zvezde nanaša kot ena koordinata, čas, določen s položajem te zvezde, pa kot druga, na prvo pravokotna koordinata. Taka mrežasta slika je presenetljivo podobna dobro znanim grafičnim metodam našega časa.

Na tej zvezdni karti iz grobnice Ramzesa VII so višine zvezd prikazane kot zaporedje koordinat, pravokotnih na ure kot na drugo zaporedje koordinat.
Preden se poslovimo od antike, je prav, da še enkrat poudarimo, kako veliko dolgujejo utemeljitelji grške geometrije Egiptu in Mezopotamiji. V stoletju Talesovega rojstva (okrog 640 - 550 pr. n. š.) je bil Milet, kjer je Tales prebival, vodilno trgovsko žarišče grško govorečih skupnosti ob obali Male Azije. Ustanovil je nič manj kot devetdeset svobodnih kolonij ob obalah Sredozemskega in Črnega morja ter trgovska naselja v samem Egiptu. Kot trdi izročilo, je Tales potoval v Egipt in se - tako kot Demokrit - naučil egipčanske geometrije, kolikor se je dalo. Vse kaže, da je potoval tudi na Vzhod, z gotovostjo pa lahko domnevamo, da sta imela Tales in Pitagora (okrog 550 - 500 pr. n. š.) stike z babilonskimi matematiki prek grških trgovinskih tekmecev Feničanov, od katerih so Grki prevzeli alfabetsko pisavo (okrog 800 pr. n. š.) in od katerih so se verjetno naučili kovati denar (ne dosti pred 600 pr. n. š.).
O ravni matematičnega znanja pri Feničanih ne vemo praktično ničesar. Prvi skupnosti teh ljudi - govorili so neki akadijskemu jeziku soroden semitski jezik - sta bila Tir in Sidon. Okrog leta 1600 pr. n. š. so priznavali nadvlado faraona Amazisa I, hetitska invazija v Sirijo kaka tri stoletja pozneje pa jih je osvobodila odvisnosti od Egipta. Prve mestne države Tir, Sidon in Biblos so pozneje prišle pod asirsko oblast (876 - 605 pr. n. š.). Še pozneje, v Talesovem času, pa pod Kaldejce (605 - 538 pr. n. š.). Tako so bila ta mesta do konca podrejenosti Egipta v živahnih stikih z mezopotamsko civilizacijo. O tem pričajo v jeziku in pisavi tedanjega Babilona napisane glinaste ploščice, ki so jih našli na njihovih tleh. Okrog leta 1000 pr. n. š. so Feničani že imeli kolonije ob španski obali, njihove ladje s tovori bakra, kositra in zlata pa so trgovale z otočjem Scilly ob angleški obali, če ne z Britanijo samo.
Taršiš iz Jonove knjige je bil feničanska kolonija v Španiji. Največja izmed vseh sredozemskih kolonij je bila Kartagina, ustanovljena leta 800 pr. n. š. Kartagina je bila daleč od središča oboževanja Baala in Astarte (pri Babiloncih sta to Bel in Ištar). Njena družbena struktura v času punskih vojn je imela določene lastnosti posvetne države, čeprav so feničanske kraljevske hiše enako kot faraoni trdile, da so božanskega izvora. Čeprav nedvomno močno pretiravamo, kadar govorimo o grško govorečih skupnostih na katerikoli stopnji njihovega obstoja kot o demokracijah, pa je med njimi in njihovimi feničanskimi učitelji pomembna razlika. Medtem ko so Feničani zadnji čuvarji svečeniške kulture v zahodnem svetu, pa Grki v Talesovem stoletju kljub vraževernosti niso bili podrejeni duhovščini in razni diktatorji, ki so se drug za drugim polaščali oligarhij v grških mestnih državah, se niso sklicevali na svoje nebeško poreklo.
Zadnji dnevi Kartagine so tudi dnevi porajanja rimske pomorske moči. Ta razbojniška družba je potolkla Arhimeda, razdejala prvo knjižnico v Aleksandriji, uzakonila gladiatorske boje in javno križanje sužnjev ter tako k naši skupni civilizaciji prispevala tiste vzvišene pojme zakona in reda, ki jih vsebuje Pax Romana in ki so vzorec za vladanje kolonistov v Keniji in Rodeziji. Scipio je dokončno izbrisal vsako sled za Kartagino (146 pr. n. š.). Če ne bi bilo tako, bi morali razmišljanju o tem, koliko dolguje jutrišnji svet ljudem različnih barv, ver in dežel, dodati nemara še eno poglavje. Tisto malo, kar vemo o deležu Feničanov, opravičuje prepričanje, da je to ljudstvo uporabilo nekatere skrivnosti babilonske astronomije v znanstveni navigaciji in zapustilo svojim grško govorečim tekmecem podlago za nov začetek.