KVADRATNA FUNKCIJA

Funkcijo 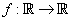, dano s predpisom

;

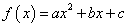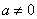
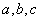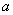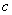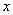imenujemo kvadratna funkcija. Števila  so koeficienti. Število  je vodilni koeficient, število  je konstantni koeficient. Kvadratna funkcija je definirana za vse realne . Izrazu 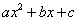 rečemo kvadratni tričlenik (trinom).

Program za izračun ničel, temena in diskriminante kvadratne funkcije.  

Graf kvadratne funkcije

Graf kvadratne funkcije se imenuje parabola in ga narišemo s pomočjo ničel funkcije, temena kvadratne funkcije, vrednosti vodilnega koeficienta in vrednosti prostega koeficienta.

Ničli kvadratne funkcije:

Ničla funkcije je točka, v kateri funkcija seka (ničle lihe kratnosti) os x ali se dotika  (ničle sode kratnosti) osi x.

Ničli kvadratne funkcije dobimo z rešitvijo enačbe 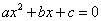. Enačbo lahko rešimo z razstavljanjem, sicer pa si pomagamo s formulo:

.

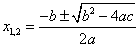Vrednost izraza pod korenom, imenujemo ga diskriminanta 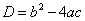, nam pove, kakšni sta ničli:

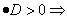V tem primeru sta ničli realni števili in sta med sabo različni, torej 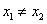; graf funkcije v obeh ničlah seka os x.

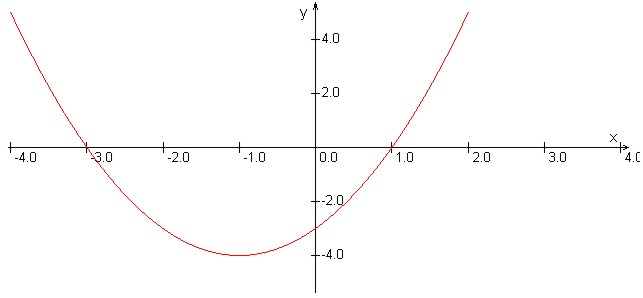
Kot primer si poglejmo graf naslednje kvadratne funkcije: 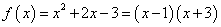. Iz drugega zapisa lahko preberemo, da ima različni ničli, in sicer 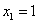 in 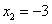. Torej graf te kvadratne funkcije seka os  v dveh različnih točkah.  

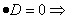 V tem primeru sta ničli enaki, takšna ničla se imenuje dvojna ničla in je realno število; na grafu se v tej ničli parabola obrne oz. se samo dotakne osi x in ne seka osi x, torej 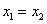; v takem primeru je dvojna ničla hkrati kar teme kvadratne funkcije.

Primer take funkcije je 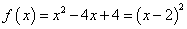. Tokrat lahko iz drugega zapisa preberemo, da ima ta funkcija dvojno ničlo (oz. ničlo lihe stopnje), in sicer 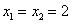. Torej se graf te kvadratne funkcije samo dotakne osi 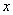, nato pa se obrne in tako v takem primeru ostane na isti strani osi .

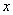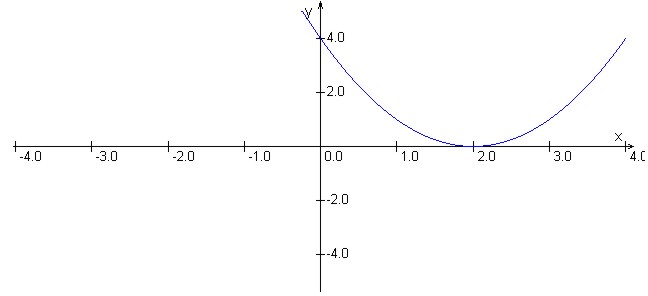
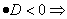 V tem primeru sta ničli konjugirani kompleksni števili; graf funkcije ne seka osi x, torej v celoti leži nad (teme kvadratne funkcije je v tem primeru minimum funkcije) osjo x ali pa pod (teme kvadratne funkcije je v tem primeru maksimum funkcije) osjo x.  

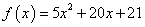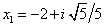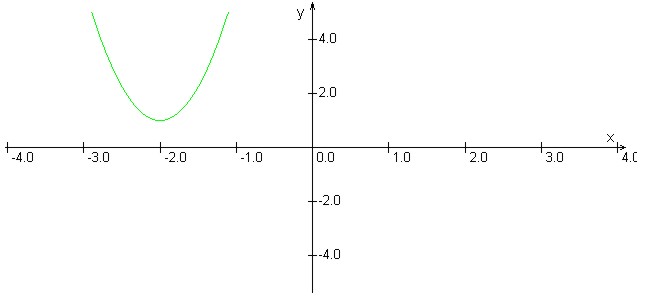
Za primer izračunajmo ničli naslednje kvadratne funkcije: , ničli lahko izračunamo kar po zgoraj navedeni formuli in dobimo  in 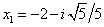. Torej ima ta funkcija konjugirano kompleksni ničli, zato graf funkcije niti ne seka abcisne osi niti se je ne dotika. Zato ves graf leži nad osjo 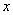 ali pa pod njo. Kje leži, je odvisno od vodilnega koeficienta, kar bomo spoznali nekoliko pozneje. V našem primeru je vodilni koeficient enak 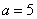, torej pozitiven in zato je graf funkcije konveksen in tako je v celoti nad osjo .   

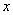Teme kvadratne funkcije:

Teme kvadratne funkcije je točka 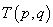. V temenu kvadratne funkcije je minimum ali maksimum kvadratne funkcije. Izračunamo ga tako, da izraz, s katerim je podana kvadratna funkcija, zapišemo v obliki popolnega kvadrata in iz tega zapisa preberemo 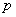 in 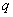; če pa tega nismo najbolj vešči, pa si lahko pomagamo s formulama za koordinati temena:

,

.

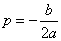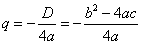Vodilni koeficient kvadratne funkcije:

Vodilni koeficient kvadratne funkcije smo v zapisu označili z 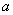( 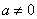, sicer ne bi imeli opravka s kvadratno funkcijo). Glede na ta, ali je 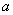 pozitiven ali negativen, vemo, kako je  parabola obrnjena oz. ali je konveksna ali konkavna.

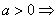 Graf kvadratne funkcije je konveksen, torej je teme minimum funkcije.

Kot smo videli že v prejšnjem primeru, bo tako tudi v tem. Vodilni koeficient naslednje funkcije 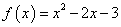 je enak 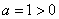, torej je graf te funkcije konveksen, in v tem primeru je teme funkcije kar minimum funkcije.  

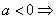Graf kvadratne funkcije je konkaven, torej je teme maksimum funkcije.

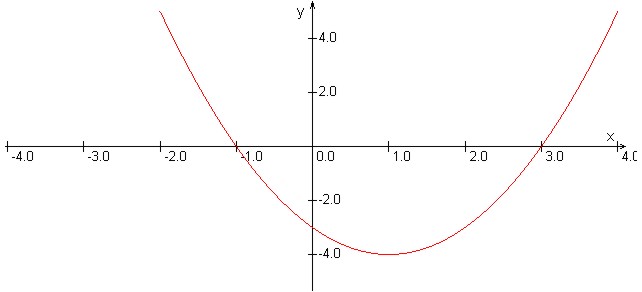
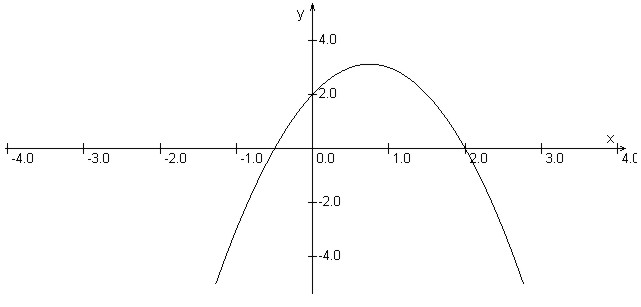
Sedaj pa si poglejmo primer kvadratne funkcije, katere graf je konkaven: 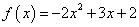. Vodilni koeficient te funkcije je enak 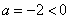, torej je graf te funkcije konkaven in teme funkcije je kar maksimum funkcije.

Nekatere zanimive povezave:

Kvadratna funkcija: http://scp.s-scptuj.mb.edus.si/~zoli/projekt/KVADRATNA.html

Dve strani z razlago matematike po področjih:

http://www.bymath.com/

http://mathworld.wolfram.com/