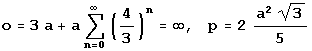PRAVOKOTNIK
PRAVOKOTNIK KVADRAT TRIKOTNIK PITAGOROV IZREK KROG
Geometrija je pomemben del človekovega življenja. Že majhni otroci v svojik slikah uporabljajo geometrijske like. Mogoče ne čisto pravilne, a vseeno. Geometrijski liki so navdihovali tudi mnoge umetnike, najbolj znan je najbrž Kandinsky. Koristna pa je tudi v vsakdanjem življenju, ko moramo ugotoviti, koliko ploščic za kopalniška tla moramo kupiti, ali tapete za novo otroško sobo. Koliko vrečk semena moramo kupiti za gredico korenja.
Večinoma se v življenju srečujemo le z osnovnimi geometrijskimi liki; s kvadrati, pravokotniki, krogi ali trikotniki, redkeje pa s kakšnimi bolj nenavadnimi oblikami. Ta stran je posvečena osnovnim geometrijskim likom, in sicer njihovim obsegom in ploščinam. Preprosto povedano nam obseg pove, najmanj kako dolgo ograjo ali vrvico potrebujemo, da objamemo nek lik. Ploščina pa nam pove, koliko barve potrebujemo, da prebarvamo lik. Ali pa koliko ploščic kvadratne oblike potrebujemo, da lik prekrijemo.
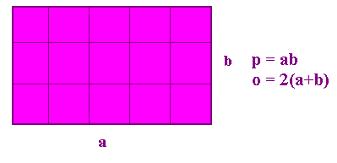
V naši okolici je gotovo največ pravokotnikov: okna hiš, gredice na vrtu, list papirja. Zato začnimo z njim:
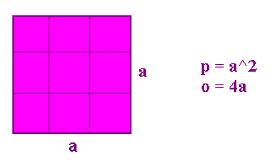
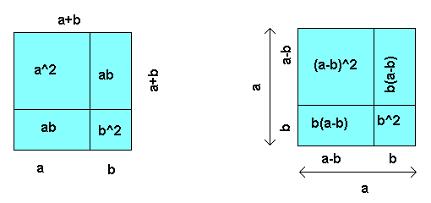
S pomočjo geometrije pa lahko pokažemo tudi stvari, ki na prvi pogled nimajo veliko zveze z liki. Formulo za kvadriranje dvočlenika lahko lepo pokažemo le s ploščino kvadrata.
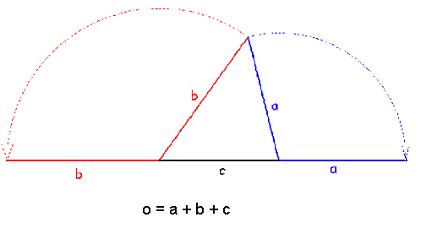
Spodnji sliki sta aktivni. To pomeni, da lahko primete poljubno točko in jo potegnete drugam. Prvotno sliko dobite s pritiskom na tipko SPACE.
Vse tri višine se sekajo v isti točki. Tej točki rečemo višinska točka. Ponavadi jo označimo s H.
Druga znamenita točka trikotnika je težišče T, ki je presek težiščnic. Težiščnice so črte, ki povezujejo oglišče z razpoloviščem nasprotne stranice trikotnika.
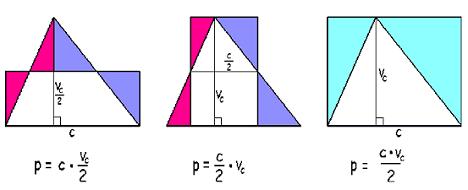
Težiščnice razdelijo trikotnik na 6 ploščinsko enakih trikotnikov. Trikotnika AC'T in C'BT sta enaka, ker imata enaki osnovnici in višini. Podobno dobimo tudi za ostale trikotnike. Tako ima vsak od teh manjših trikotnikov ploščino, ki predstavlja 1/6 ploščine celega trikotnika.
Imenuje se po grškem matematiku, ki je živel na otoku Samos. Izrek najdemo že v velikem Evklidovem učbeniku, poznali pa so ga tudi Kitajci. Morda so ti izrek sami odkrili, morda pa so - kot Pitagora - zanj zvedeli od Babiloncev, ki so imeli zelo razvito matematiko.
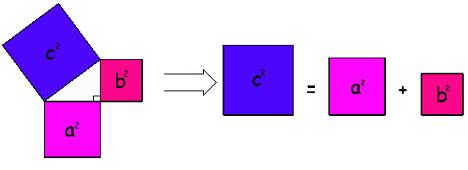
Izrek dokažemo na precej preprost način:
 |
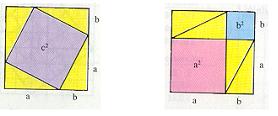Vidimo, da so na obeh slikah štirje pravokotni trikotniki s katetama a in b. Torej je res c2 = a2+b2. |
Obstaja pa še en zanimiv dokaz:
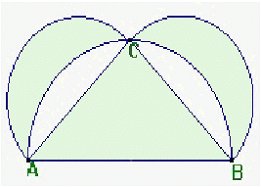
Najbrž najbolj zanimive pa so gotovo naloge, kjer sta ploščini navidezno enakih likov različni. Tu sta dva primera:
Avtor drugega problema je predavatelj matematike v Oxfordu Lewis Carroll, ki je tudi avtor popularne knjige Alice v čudežni deželi.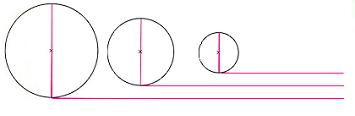
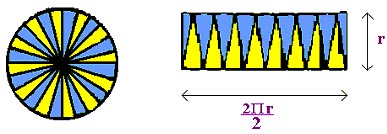
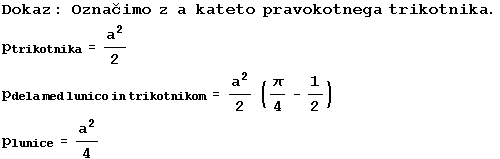
Krogi pa so pogosti tudi v arhitekturi in umetnosti, saj z njimi lahko naredimo zanimive vzorce.
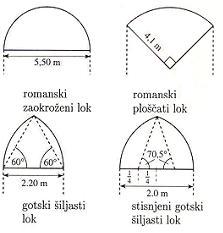
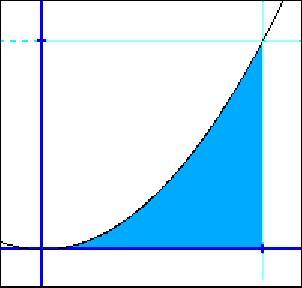
Tu smo si ogledali le štiri osnovne geometrijske like. Vsi vemo, da je takih primerov se veliko več. Za vse je težko izračunati ploščino in obseg. Nekaj jih lahko izračunamo s pomočjo integrala. Če znamo krivuljo opisati s funkcijo, potem lahko izračunamo njeno dolžino in ploščino lika, ki ga oklepa.
Ploščino lika pod parabolo lahko aproksimiramo s pomočjo vsote ploščin pravokotnikov, ki so včrtani pod parabolo ali pa nad njo. Govorimo o t.i. spodnjih s in zgornjih vsotah S. Spodnje vsote se s povečevanjem števila včrtanih pravokotnikov povečujejo, zgornje pa zmanjšujejo. Vedno pa je vsaka spodnja vsota navzgor omejena z vsako zgornjo vsoto, vsaka zgornja vsota pa navzdol omejena z vsako zgornjo vsoto. Imamo torej naraščajoče navzgor omejeno zaporedje spodnjih vsot in padajoče navzdol omejeno zaporedje zgornjih vsot. Obe zaporedji imata limito, ki je tudi hkrati iskana ploščina.
