Tudi Johann BERNULLI se je problema brahistohrone lotil intuitivno, njegov pristop je bila analogija z lomnim zakonom. Pri svojem prikazu se je opiral na zakone optike.

Eden najosnovnejših je zakon o odboju in lomu svetlobe.

Vemo, da svetloba vedno potuje po premicah, kar z drugimi besedami pomeni, da svetloba vedno izbere najkrajšo pot. To dejstvo je omogočilo Heronu iz Aleksandrije, da je v prvem stoletju našega štetja razložil odbojni zakon – enakost vpadnega in odbojnega kota.

Lom svetlobe se od odboja med drugim razlikuje tudi po tem, da pri odboju hitrost svetlobe ostane nespremenjena, medtem ko se pri lomu hitrost spreminja kot funkcija lomnega količnika n v snovi. Načelo, da se svetloba giblje po najkrajši poti, sedaj zapišemo v obliki Fermatovega načela, ki pravi, da svetloba izbere najhitrejšo pot. Fermatovo načelo je v homogeni snovi, kjer je hitrost svetlobe konstantna, ekvivalentno prvemu načelu.

Opomba: Kasneje ugotovijo, da svetloba v resnici potuje tako, da minimizira akcijo in ne časa ali dolžine poti.

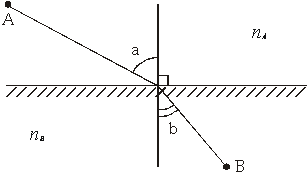
Na zgornji sliki pot svetlobe od točke A do točke B ni daljica AB. Zaradi prehoda iz snovi s količnikom n_A v snov s količnikom n_B, pride do loma. Tako je pot svetlobe enaka zlomljeni črti, katero svetloba prepotuje v najkrajšem času med vsemi možnimi potmi med točkama A in B. Povezava med vpadnim in odbojnim kotom ter ustreznima hitrostima je podana z enačbo:

   ,

ki pa je ekvivalentna lomnemu zakonu:

  (to formulo je prvi pravilno razložil Fermat).

Primer nehomogenega medija, kjer najkrajša pot ni najhitrejša, se pojavi tudi v mehaniki, kjer v navpični smeri deluje težnost. To je izhodišče Jeanu Bernulliju pri reševanju problema brahistohrone.

Svojo rešitev je dokazal v Acta Eruditorium leta 1697.

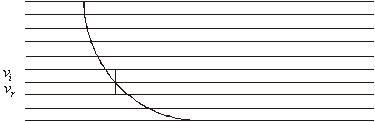
Prostor si je zamislil kot razrezan v tanke plasti, tako tanke, da smemo predpostaviti, da je hitrost znotraj posamezne plasti konstantna. Znotraj vsake plasti trajektorija postane najkrajša izmed poti in zato nujno daljica. Celotno trajektorijo tako sestavlja zaporedje daljic. Opisati moramo le še način, kako se premikamo iz ene plasti v drugo. Želimo si namreč optimizirati čas potovanja. To storimo s pomočjo Fermatovega načela. Torej, če je v_i hitrost v dani plasti in v_r hitrost v plasti tik pod njo, potem sta kot i, ki ga oklepa trajektorija z vertikalo v prvi plasti, in kot r v sosednji plasti, povezana z lomnim zakonom:

.

Če sedaj vodoravne trakove tanjšamo, njihovo število narašča v neskončnost in zaporedje daljic se približuje krivulji. Tangente v vsaki točki te krivulje se približajo zaporedju daljic. Povezava med kotom u, ki ga tangenta oklepa z navpičnico, in hitrostjo je v tem primeru podana z enačbo:

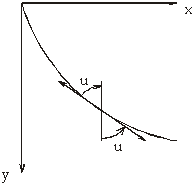
Hitrost delca poznamo: .

In tako pridemo do enačbe:

To pa je karakteristična enačba cikloide. Cikloida je pot, ki jo naredi žebelj na obodu kolesa, ko se to normalno kotali, iz začetne točke, ko zapusti tla, dokler ga, po končanem polnem zasuku, stalno gibanje kolesa ne prenese nazaj na tla.

Kako vidimo, da cikloida ustreza enačbi ?

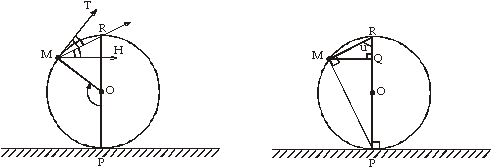
Potovanje točke M na cikloidi povzročata dve gibanji: vrtenje kolesa okrog osi O (posledica je gibanje točke M v smeri tangente MT) in horizontalna translacija (povzroči premik točke M v vodoravni smeri MH). Ker se kolo vrti brez podrsavanja, sta omenjena premika enakih dolžin in zato tangenta cikloide razpolavlja kot HMT ter gre skozi točko R, ki je diametralno nasprotna dotikališču kolesa s tlemi.

Dobimo: ,

iz česar sledi:

(r je radij kroga). Ta enačba pa je ekvivalentna enačbi

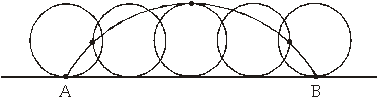
Sedaj, ko je Bernulli dokazal, da je iskana krivulja obrnjena cikloida, pa se nam porodi vprašanje, kako konstruirati cikloido, ki se začne v A in konča v B.

To vprašanje je rešil Newton leta 1697:

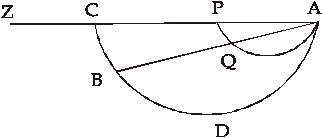
Naloga: Potrebno je poiskati krivuljo ADB, po kateri se bo utež, pod vplivom sile teže, najhitreje spustila iz poljubne dane točke A v poljubno dano točko B.

Rešitev: Iz dane točke A narišemo neomejeno premo črto APCZ, vzporedno vodoravnici in iz točke A poljubno cikloido AQP, ki seka daljico AB v točki Q, in nato drugo cikloido ADC, katere osnovnica in višina sta v enakem razmerju z osnovnico in višino cikloide APQ, kot je AB z AQ. Slednja cikloida bo šla skozi točko B in bo predstavljala tisto pot, vzdolž katere se masa pod vplivom težnosti najhitreje spusti iz točke A v točko B.

Čeprav je Jean Bernulli pravilno ugotovil, da je brahistohrona obrnjena cikloida, pa njegova metoda, ki temelji na analogiji, deluje le v posebnem primeru in z njo ni mogoče reševati splošnejših sorodnih problemov. Na to je prvi opozoril Johannov starejši brat Jakob Bernulli, ki je problem brahistohrone razširil z novimi vprašanji. Jakobova rešitev.