
Cikloidne krivulje
Ker je rešitev problema brahistohrone cikloida, je prav, da povemo še nekaj o cikloidnih krivuljah. V to skupino krivulj sodijo:
Krivulja, ki jo popiše točka krožnice, kotaleče se po premici, ne da bi pri tem drsela. Enačba v prametrični obliki:
x = a (t - sin t) y = a(1 - cos t) |


Poglej FILM.
Krivulja,
ki jo popiše točka krožnice, kotaleče se po drugi krožnici zunaj nje, ne da
bi pri tem drsela.
Parametrična enačba:
x = (R + r)cos t –r cos((R + r) t/r) y= (R + r)sin t –r sin((R + r) t/r) |
R- polmer nepremičnega, r-polmer premičnega kroga.
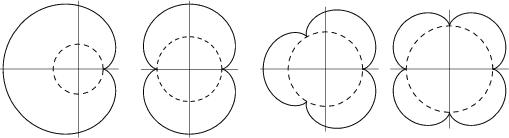
r = R, r = R/2, r = R/3, r = R/4
Označimo m = R/r.Slike epicikloid z različnim m:
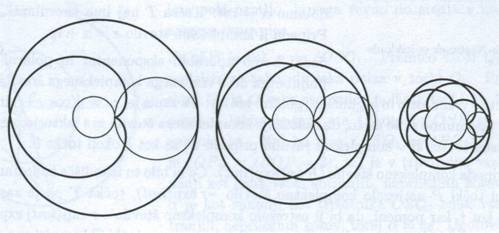
m = 2, m = 3/2, m = 3/5
Kardioida je primer epicikloide za m = 1. Kardioido opiše poljubna točka na krožnici, ki se kotali po zunanji strani enako velike krožnice.Če v parametrično enačbo epicikloide vstavimo R = r in m = 1, dobimo
| x = 2rcost – rcos2t y = 2rsint – rsin2t |
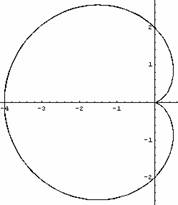
Krivulja ima ost v točki (r,0).V polarnih koordinatah je njena enačba r = 2r (1 - cost). V kartezičnih koordinatah pa dobimo enačbo četrte stopnje: (x2 +y2+ 2rx) – 4r2(x2 + y2) = 0.
Krivulja, ki jo popiše točka krožnice, kotaleče se po drugi krožnici znotraj nje, ne da bi pri tem drsela. Parametrična enačba:x = (R - r)cos t +r cos((r - R) t/r)y= (R - r)sin t +r sin((r - R) t/r)
Slike za različne m:
| m=1/2 | m=1/3 | m=1/4 | m=1/5 |
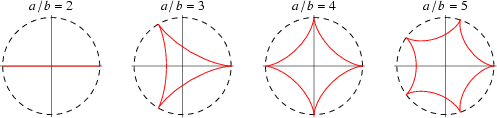
To je hipocikloida za m = ¼. Iz parametričnih enačbe za hipocikloido dobimo x =R cos3(t/4) in y = R sin3(t/4).
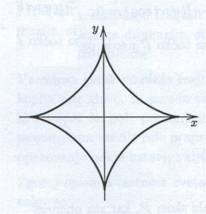
Pri navadni asteroidi zamenjamo t z 4t in dobimo x = R cos3t in y = R sin3t. To enačbo lahko pretvorimo v implicitno obliko: x2/3 + y2/3 – R2/3 = 0. Če se znebimo še korenov, dobimo enačbo šeste stopnje: (x2 + y2 – R2)3 + 27 R2x2y2= 0.
| Na začetek |