UVOD

Velikost dimenzij likov ali predmetov lahko odmerimo: velikost določimo z merjenjem. Določitev velikosti je lahko zelo natančna, če jo določimo z mero: mm, cm, dm, m, km,...

Velikost dimenzij lahko določimo tudi s primerjanjem velikosti dimenzij po občutku. Takšno določanje velikosti ni najbolj natančno. Primerjavo odnosov dveh ali več velikosti bodisi z merjenjem ali z določanjem na oko imenujemo sorazmerje ali proporc. Upoštevana pravila razmerja so hitro vidna, opazi jih vsakdo, ki ima malo izurjeno oko. Pritegnejo pa tudi vsakogar, ki se ukvarja z uporabljanjem ali oblikovanjem predmetov in prostora, torej slikarja, kiparja ali arhitekta, kajti pravilno sorazmerje močno učinkuje na opazovalca.

Razmerja so torej odnosi med velikostmi znotraj neke oblike (forme) ter odnosi med velikostmi več oblik v kompoziciji.

Vsak začetek v komponiranju oblik v kompoziciji je določanje razmerij. Cilj vsake uskladitve pa je doseči zanimivost in ohraniti celoto. Že ko izbiramo format, določamo medsebojno razmerje dolžine in širine. Odnosi med velikostmi elementov v kompoziciji so pomemben dejavnik pri usklajevanju neke oblike v celoto, tako na risbi, kipu ali stavbi.

Velikosti lahko nizamo na enake ali neenake dele. Vendar pa so neenaki deli bolj razgibani in zato zanimivejši od enakih. Eno od takih pravilnih razmerij v kompoziciji risbe, slike, kipa, stavbe ali tudi fotografije, ki daje izrazito asimetričen vtis, je zlati rez.

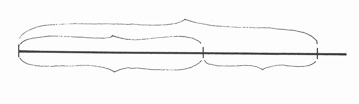
Geometrično gre za delitev neke dolžine (daljice) na dva različna dela, in sicer tako, da je razmerje manjšega dela daljice do večjega dela enako kot razmerje večjega dela daljice proti celotni dolžini (prikazano na sliki 1).

SLIKA 1

To je torej idealno sorazmerje, v katerem je vsaka različna velikost v istem razmerju tako do nadrejene kot do podrejene velikosti.

KONSTRUKCIJA

Do tega pravila o sorazmerju zlatega reza smo prišli po občutku, lahko pa ga podpremo geometrijsko, tako da z ravnilom in šistilom (konstrukcijsko) obdelamo daljico.
Poljubno daljico AB razdelimo na dva enaka dela. Dolžino polovice daljice prenesemo na pravokotno premico iz A in dobimo daljico AC. Tocko C povežemo z B in dobimo daljico BC, tako da nastane pravokotni trikotnik z oglišči ABC. S šestilom prenesemo dolžino daljice AC na daljico CB in dobimo A1. Iz točke B odmerimo s šestilom dolžino daljice BA1 in jo prenesemo na daljico AB; tako dobimo točko D. Na daljici AB nastaneta dve daljici AD in DB (prikazano na sliki 2).

SLIKA 2

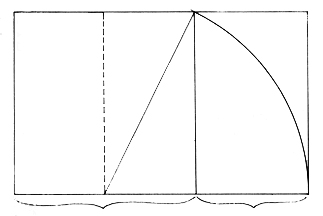
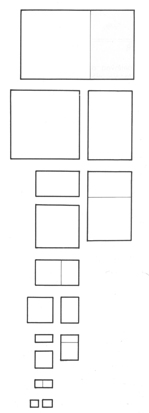
V geometriji je to takšna delitev daljice na dva različna dela, da je razmerje MANJŠI : VEČJI = VEČJI : CELOTA. To razmerje lahko izrazimo tudi s številkami, in sicer gre za razmerje 1: 1,6180339887... Če ti dolžini prenesemo na risalno ploskev, kjer ima pomembno vlogo površina, dobimo pravokotnik v "idealnem" razmerju. Stranica pravokotnika (manjša : večja) sta si v razmerju, ki se mu pravi zlati rez.
Če je lepoto zlatega reza mogoče utemeljevati v matematični ubranosti delov do celote, potem lahko torej tudi površino ¨zlatega prevokotnika¨ razdelimo na dva različna dela, ki sta v idealnem razmerju (zlatem rezu).

Narišemo ga tako, da narisani kvadrat razdelimo na dva enaka dela – pravokotnika. Drugemu pravokotniku narišemo diagonalo in njeno dolžino prenesemo s šestilom na podaljšano daljico kvadrata. Novonastala dolžina predstavlja dolžino pravokotnika. Velikosti novonastalega pravokotnika in kvadrata sta medsebojno ¨v zlatem rezu¨ (prikazano na sliki 3).

SLIKA 3

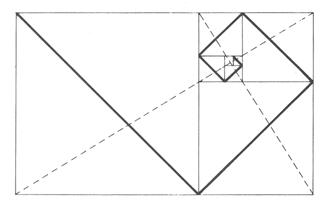
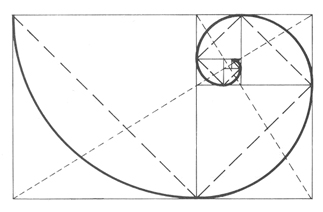
Nastalemu manjšemu pravokotniku lahko spet vrišemo kvadrat, in tako nastaneta znotraj tega pravokotnika spet nov pravokotnik in kvadrat, katerih velikosti sta si spet v idealnem razmerju – zlatem rezu. Taka delitev se lahko nadaljuje še kar naprej in naprej, zato govorimo o neskončni delitvi (prikazano na sliki 4).

SLIKA 4

SPIRA MIRABILIS

Če prek kvadratov povlečemo diagonale, dobimo ¨zlato spiralo¨ ali spira mirabilis ali logaritemska spirala, ki je lahko oglate oblike (prikazano na sliki 5), če pa diagonalo razširimo v lok, bo spirala mehkejša – zaobljena (prikazano na sliki 6).

SLIKA 5

SLIKA 6

Spira mirabilis ima lastnost, da vsaka ravna črta iz središča spirale seka spiralo pod istim kotom. Pojavlja se v mnogoterih oblikah od spiral v cvetu soncnič, školjk, polžjih hišic, rogov, čekanov, pajkovih mrež in oddaljenih spiralnih galaksij. Ime spirala mirabilis lat. (čudežna spirala) je dobila logaritemska spirala od velikega matematika Jakoba Bernoulli-ja, zaradi njenih čudovitih lastnosti.

POSTAVITEV

Če površino pravokotnika razdelimo horizontalno in vertikalno v zlatem rezu, dobimo na sečišču dolžine in višine optično središče zlatega reza (prikazano na slikah 7, 8).

SLIKA 7

SLIKA 8

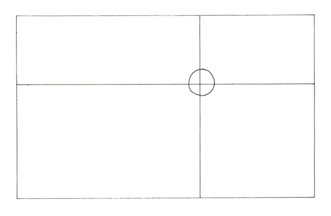
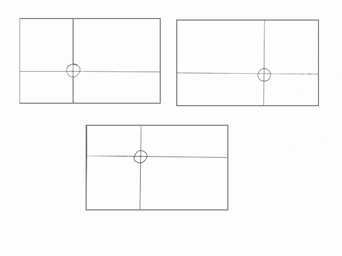
To središče zlatega reza pa lahko vrišemo tudi v nasprotno stran pravokotnika, na primer na levo, pa tudi na spodnjo stran. Tako lahko rečemo, da ima vsaka pravokotna ploskev po štiri točke zlatega reza (prikazano na sliki 9).

SLIKA 9

Podobne štiri točke zlatega reza lahko narišemo tudi na kvadratnemu formatu (prikazano na sliki 10).

SLIKA 10

Ugotovimo lahko, da ima vsaka pravokotna ploskev oziroma format po štiri točke zlatega reza. Slikarji v te točke postavljajo glavnega junaka ali pač tisti del dogajanja na sliki, na katerega želijo usmeriti pozornost. Slikar uporablja pravila zlatega reza (dolžine do višine risbe ali slike) v kompozicijski razdelitvi in pri vnašanju likov, saj vsako risanje ali slikanje začenja s formatom in z vnašanjem oblik, ki jih po velikosti in obliki določi v skladu z idejo oziroma motivom, ki ju želi upodobiti.
Uporablja eno, dve, tri ali vse štiri točke zlatega reza (prikazano na slikah 11, 12, 13, 14).

SLIKA 11

SLIKA 12

SLIKA 13

SLIKA 14

UPORABA

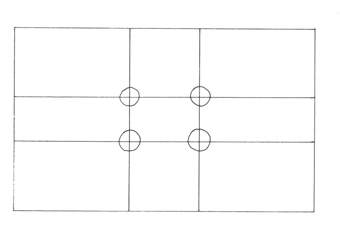
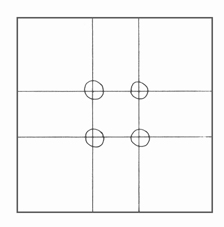
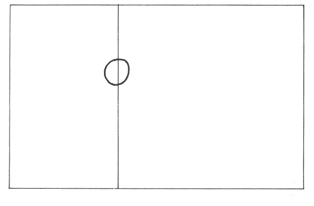
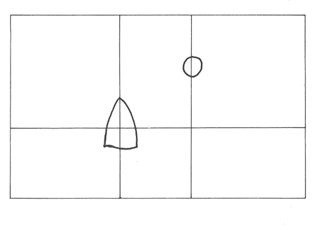
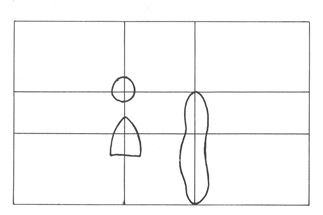
Kadar vrisuje ali slika na površino en element, ga bo postavil v točko – v optično središče, da bo dosegel ravnovesje v kompoziciji. Podobno razvrsti tudi dva elementa na risarsko površino, pri razvrstitvi treh ali štirih elementov pa lahko doseže razvrestitev okrog središča celotne površine (prikazano na slikah 15, 16, 17).

SLIKA 15

SLIKA 16

SLIKA 17

Pokrajinski motivi so mnogokrat upodobljeni tako, da risalni list deli horizontalna črta zlatega reza, ki sovpada z začetkom ali koncem pokrajine, v vertikali pa je naslikano drevo ali steber (prikazano na sliki 18).

SLIKA 18

V zlaten rezu so razdeljeni tudi svetlobni barvni odnosi na risbi ali sliki, enako tudi razmerje med toplo in hladno površino (prikazano na sliki 19) ali med pestro in manj pestro barvo (prikazano na slik 20).

SLIKA 19

SLIKA 20

Velikokrat pa razdelitev risbe ali slike v zlatem rezu ne poteka povsem vodoravno. Horizontala se lahko rahlo dviga nad črto zlatega reza, na drugi strani pa se spušča na spodnjo stran (prikazano na slikah 21, 22, 23, 24).

SLIKA 21

SLIKA 22

SLIKA 23

SLIKA 24

Zlatega reza ne poznajo samo slikarji, temveč tudi fotografi: še posebej je zlati rez razširjen pri umetniški fotografiji (prikazano na sliki 25).

SLIKA 25

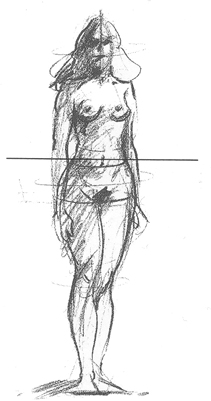
Ravno tako tudi kiparji pri oblikovanju kipov upoštevajo sorazmerje zlatega reza, posebej pri zgradbi človeškega telesa (prikazano na sliki 26).

SLIKA 26

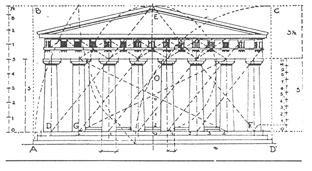
Zelo pomemben je tudi zlati rez v arhitekturi. Razmerje so poznali že Egipčani pri gradnji piramid, saj je osnovnica (horizontala) piramide v zlatem rezu proti širini. Stari Grki so v zlatem rezu zidali stavbe in oblikovali posode (prikazano na sliki 27).

SLIKA 27

V začetku 16.stoletja je Italijan Fra Luca Pacioli razglasil razmerje zlatega reza za ¨božansko razmerje¨. (Ime zlati rez je dobilo leta 1830.) Dosledno upoštevanje in ponavljanje zlatega reza v risbi, sliki, kipu, stavbi in fotografiji pa lahko privede do monotonosti, stereotipnosti.
Tudi v naravi srečujemo zlati rez. Kar se tiče človeškega telesa, je tista meja, ki določa zlati rez, popek (prikazano na sliki 28).

SLIKA 28

Tudi zgradba mehkužcev in lupinarjev je v zlatem rezu – sipa, hobotnica, morska školjka (prikazano na sliki 29).

SLIKA 29

V rastlinskem svetu pa sta si, na primer, v zlatem razmerju deblo in krošnja.

Zlati rez pa je tudi zelo uporaben pri oblikovanju plakatov, knjižnih naslovnic, drobne embalaže (prikazano na sliki 30).

SLIKA 30