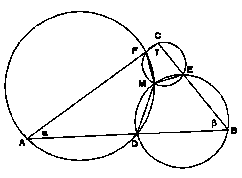| NEKAJ ZNAMENITIH TOČK TRIKOTNIKA, EULERJEVA PREMICA IN EULERJEVA KROŽNICA
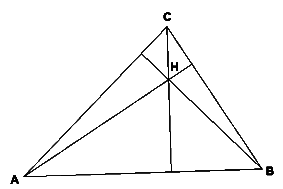
Dokaz: Za izhodišče O koordinatnega sistema vzemimo središče trikotniku očrtane krožnice. Naj bodo a, b in c krajevni vektorji oglišč trikotnika. Velja |a| = |b| = |c|. Dokažimo, da je točka H s krajevnim vektorjem h = a + b + c višinska točka trikotnika ABC. Oglejmo si skalarni produkt vektorjev BA in CH. Velja BA · CH = (h-c)·(a-b)
= (a+b)·(a-b) = 0. Od tod sledi, da je premica skozi
točki H in C 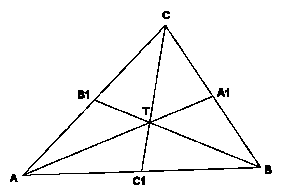 V ta namen najprej vpeljimo pojem
Cevove linije in navedimo (brez dokaza) Cevov izrek.
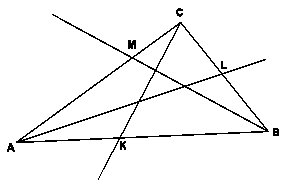
Definicija: Cevova linija
je premica, ki poteka skozi oglišče trikotnika, a ni enaka nosilki sosednjih stranic.
V ta namen najprej vpeljimo pojem
Cevove linije in navedimo (brez dokaza) Cevov izrek.
Definicija: Cevova linija
je premica, ki poteka skozi oglišče trikotnika, a ni enaka nosilki sosednjih stranic.
 Vpeljimo nekaj oznak:
K, L in M naj bodo
presečišča Cevovih linij z nosilkami stranic AB, BC in AC (kot na sliki).
Vpeljimo nekaj oznak:
K, L in M naj bodo
presečišča Cevovih linij z nosilkami stranic AB, BC in AC (kot na sliki).
In še: k := AK/KB; l :=BL/LC; m :=CM/MA. Velja naslednji Cevov izrek: Potrebni in zadostni pogoj za to, da gredo tri Cevove linije danega trikotnika (ki potekajo vsaka skozi svoje oglišče) skozi isto točko ali da so vzporedne je veljavnost zveze k × l × m = 1. Dokaz (da težišče trikotnika obstaja): Težiščnice trikotnika so Cevove linije. Velja k := AC1/C1B = 1 l :=BA1/A1C = 1 m :=CB1/B1A = 1 Te enakosti sledijo iz definicije težiščnice.Produkt k × l × m je torej enak 1, težiščnice očitno niso vzporedne torej se sekajo v skupni točki – težišču trikotnika. QED Za aktivno grafično predstavitev klikinite tukaj.
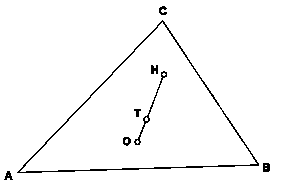
Naj bo ABC poljuben trikotnik in naj bodo točke A1, B1 in C1 razpolovišča stranic trikotnika, točka T pa težišče. Za izhodišče si izberimo poljubno točko v ravnini (označimo je z O'). a, b in c naj bodo krajevni vektorji oglišč trikotnika. Velja: CC1 = 1/2(a+b) – c = 3/2 (1/3 (a+b+c) – c). Točko s krajevnim vektorjem 1/3(a+b+c) označimo s T1. Zgornja enakost se potem glasi CC1=3/2 CT1 in od tod sledi, da T1 leži na težiščnici tc. Velja tudi AA1 = 3/2 (1/3 (a+b+c) –a) = 3/2 AT1 in od tod sledi, da točka T1 leži tudi na težiščnici ta. S podobnim premislekom ugotovimo, da točka T1 leži tudi na težiščnici tb. Točka T1 je torej težišče T trikotnika. V posebnem primeru, ko za
izhodišče O' vzamemo središče trikotniku očrtane krožnice O velja
poleg enakosti Dokazali smo izrek: V poljubnem trikotniku so središče očrtane krožnice, težišče in višinska točka kolinearne točke. Njihova nosilka je Eulerjeva premica, odsek OH pa Eulerjeva daljica. Točki O in H ležita na isti strani točke O in velja še OT = 1/3OH.
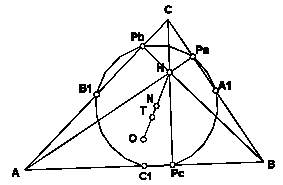
Opomba: Če višinska točka H in središče O trikotniku očrtane krožnice sovpadata, Eulerjeva premica ne obstaja. QED Za aktivno grafično predstavitev klikinite tukaj. EULERJEVA (FEUERBACHOVA) KROŽNICA TRIKOTNIKA Trditev: Razdalja med razpoloviščem N Eulerjeve daljice in razpoloviščem poljubne stranice trikotnika je r/2, kjer je r polmer trikotniku očrtane krožnice. Krožnico s središčem v N in polmerom r/2 imenujemo Eulerjeva krožnica trikotnika in poteka tudi skozi podnožišča višin trikotnika.
Dokaz: Privzeli bomo oznake, ki smo jih uporabljali do sedaj. Ker je O središče trikotniku očrtane krožnice, je |a| = |b| = |c| = r. Velja |NA1| = |1/2(b+c) – 1/2(a+b+c)| = |-1/2a| = r/2 in podobno |NB1| = |1/2(a+c) – 1/2(a+b+c)| = |-1/2b| = r/2 ter |NC1| = |1/2(a+b) – 1/2(a+b+c)| = |-1/2c| = r/2. Dokaz, da Eulerjeva krožnica poteka tudi skozi podnožišča višin, bomo opustili.QED Za aktivno grafično predstavitev klikinite tukaj. Miguelov izrek: Naj bo dan poljuben trikotnik ABC in na vsaki stranici po ena izbrana točka različna od oglišč. Konstruiramo tri krožnice, katerih vsaka poteka skozi eno oglišče in skozi tisti dve od izbranih točk, ki ležita na stranicah, ki se stikata v tem oglišču. Potem imajo vse tri krožnice skupno točko, ki jo imenujemo Miguelova točka trikotnika. Dokaz: Izbrane točke na stranicah trikotnika označimo z D, E in F (tako kot na sliki). Denimo najprej, da točka M leži v notranjosti trikotnika ABC. Štirikotnik ADMF je tetiven (njegove stranice so tetive iste krožnice), zato velja < DMF = p - a . Štirikotnik BDME je prav tako tetiven, zato velja tudi < DME = p - b . Sledi < EMF = 2p - (p - a + p - b ) = a + b = p - g . Štirikotnik CEMF je torej tudi tetiven (velja: štirikotnik je tetiven natanko tedaj, ko sta nasprotna kota suplementarna) in zato krožnica, ki poteka skozi točke C, E in F vsebuje tudi točko M. Denimo sedaj, da točka M leži zunaj trikotnika ABC. 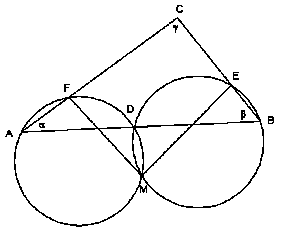 Velja < DBE = < DME = b , saj gre za obodna
kota nad istim lokom.
Velja < DBE = < DME = b , saj gre za obodna
kota nad istim lokom. Podobno < FAD = < FMD = a . Sledi < FME = a + b = p - g in od tod tetivnost štirikotnika CEMF. Točka M torej tudi v tem primeru leži na krožnici skozi točke C, F in E. 2. Ostane nam še primer, ko se krožnici K(A,D,F) in K(B,E,D) samo dotikata. 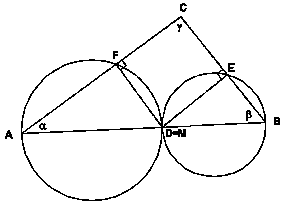 Očitno je dotikališče točka D.
Izkaže se, da je tudi v tem primeru štirikotnik CEMF tetiven, zato tudi krožnica
skozi točke C, E in F vsebuje točko D.
QED
Za aktivno
grafično predstavitev klikinite tukaj.
[Domov] [Nazaj]
Očitno je dotikališče točka D.
Izkaže se, da je tudi v tem primeru štirikotnik CEMF tetiven, zato tudi krožnica
skozi točke C, E in F vsebuje točko D.
QED
Za aktivno
grafično predstavitev klikinite tukaj.
[Domov] [Nazaj] |