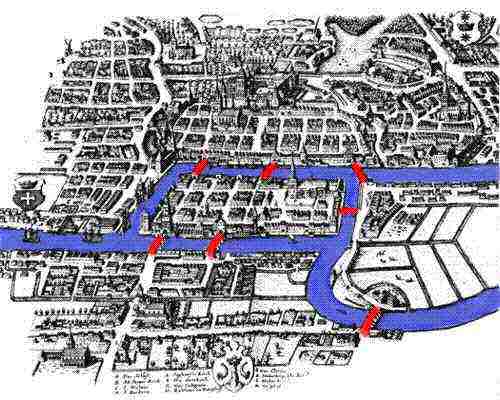
Eulerjev problem
V 18. stoletju je bilo v srednjeveškem mestu Königsberg v Vzhodni Prusiji sedem mostov, ki so povezovali štiri dele mesta. Na reki Pregel je bil otok, imenoven Kneiphof. Reka se je, kot kaže slika, razcepila v dva rokava. Pravijo, da so se meščani zabavali s poskušanjem, ali bo komu uspelo sprehoditi se po mestu tako, da bo prečkal vsakega od mostov natanko enkrat in se vrnil na začetno točko.
Meščani so zaman znova in znova poskušali najti obhod mesta, ki bi prečkal vsakega od mostov natanko enkrat in se vrnil v izhodišče, in so začeli verjeti, da naloga nima rešitve. Dokazati tega ni znal nihče, vse dokler se problema ni lotil Leonard Euler. Eulerjev dokaz je bil objavljen leta 1736 v članku z naslovom Solutio problematis ad geometriam situs pertinensis.
Na problem königberških mostov lahko pogledamo kot na problem iz teorije grafov, pri čemer so točke štirje deli mesta, povezave grafa pa sedem mostov na reki. Problem iskanja obhoda grafa , pri katerem "prehodimo" vsako povezavo natanko enkrat imenujemo iskanje Eulerjevega obhoda v tem grafu.
Euler v članku ni obravnaval samo problem königsberških mostov, ampak se je lotil tudi bolj splošnih porazdelitev delov mesta in mostov. Ideje, ki jih je uporabil so zelo blizu idejam teorije grafov, zato Eulerjev članek (čeprav ni napisan v takem jeziku) štejemo za prvi članek teorije grafov.
V jeziku teorije grafov lahko problem königsberških mostov povemo takole: štirje deli mesta naj bodo točke grafa, sedem mostov pa sedem povezav.
Poiskati moramo enostaven obhod grafa, na katerem so vse povezave grafa. Problem je po Eulerju dobil ime "iskanje Eulerjevega obhoda v grafu". Lotimo se torej iskanja Eulerjevega obhoda na grafu.
Kdaj bo v grafu obstajal Eulerjev obhod?
Vidimo lahko, da mora vsakič, ko "obiščemo" neko točko obstajati možnost, da to točko tudi "zapustimo" po drugi povezavi. Zato mora imeti v Eulerjevem grafu vsaka točka sodo stopnjo. Velja celo več, kar bomo sedaj tudi pokazali:
Izrek: Naj bo G povezan graf. Če je G Eulerjev, so vse točke sode stopnje in obratno, če so vse točke sode stopnje, je graf Eulerjev.
Dokaz: O prvem delu dokaza smo že razmislili tik pred izrekom, drugega pa dokažemo z indukcijo na število povezav.
Sedaj lahko že vidimo, da königsberški problem nima rešitve (saj graf vsebuje točke lihe stopnje).
Za primer, kateri graf je Eulerjev, si oglejmo naslednje štiri grafe:
Najprej si oglejmo kar graf, ki smo si ga ogledali že v uvodu:
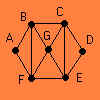
Za njega smo ugotovili, da je tako Eulerjev kot Hamiltonov. Pa sedaj ta graf nekoliko preoblikujmo in poglejmo kaj dobimo:
|
Graf (a) je Eulerjev, saj vsebuje Eulerjev obhod BCGFEGB. Drugi graf (b) ni pa Eulerjev, ravno tako kot tudi zadnji graf (c).
Iz uvodnega raziskovalčevega problema, lahko dobimo tudi nekaj zelo zanimivih ugank in nalog iz zabavne matematike (ki si jih bomo v nadaljevanju tudi nekoliko pobližje ogledali), najdejo pa se tudi čisto pravi problemi, kot je na primer iskanje najkrajše poti pri čiščenju snega v večjem mestu...
Poskusimo narisati dani diagram s čim manj potezami in pri tem paziti, da kakšen del ne narišemo dvakrat. Tako je na primer spodnji diagram čisto preprosto narisati s štirimi potezami. Toda, ali se ga da narisati tudi z manj (s tremi potezami)?

Leta 1809 je L. Poinsot pokazal, da se da diagrame z n-paroma povezanimi točkami narisati z eno samo potezo, če je n lih.
Za lažje razumevanje si poglejmo nekaj preprostih primerov (kdor želi, lahko grafe, ki se dajo narisati z eno samo potezo, tudi sam nariše):
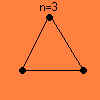 da da 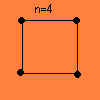 ne ne 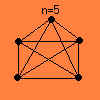 da da  ne ne  da da |
V jeziku teorije grafov to lahko povemo tako: polni graf Kn (to je graf, v katerem nastopajo vse možne povezave med točkami) je Eulerjev samo za lihe vrednosti n, kot sledi iz zgornjega izreka.
Kot bomo v nadaljevanju videli, se da graf predstaviti tudi s pomočjo domin.
Pa si oglejmo: Vemo, da je poln graf K7 Eulerjev, saj imajo vse njegove točke sodo stopnjo. Če sedaj točke grafa označimo z 0,1,2,3,4,5 in 6, potem dobimo Eulerjev obhod, če povezave prehodimo v naslednjem vrstnem redu:
10, 12, 23, 34, 45, 56, 60, 02, 24, 46, 61, 13, 35, 50, 03, 36, 62, 25, 51, 14, 40.
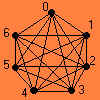
Vsaki od teh povezav lahko priredimo domino - povezavi 12 na primer ustreza domina:
![]()
Zgornjemu Eulerjevemu obhodu torej ustreza razporeditev običajne igre z dominami, z izjemo podvojenih (00, 11, 22, 33, 44, 55, 66), vendar ko za graf najdemo pravo zaporedje domin, lahko dvojne domine vrinemo na primerna mesta ter s tem pokažemo, da je popolna postavitev domin mogoča. Zgornjemu Eulerjevemu obhodu ustreza tako naslednja postavitev domin:
|
Nazadnje si poglejmo še problem iskanja izhoda iz labirinta.
Za točno kakšen problem gre in kakšna je povezava z Eulerjevimi grafi si lahko ogledamo na primeru labirinta imenovanega Hampton Court.
Če si narišemo zemljevid labirinta, ga lahko predstavimo kot graf tako, da označimo vse možne povezave na križiščih. Pri labirintu Hampton Court imamo tako v točki B dve možnosti, lahko gremo v C ali v D. Če tako premislimo na vsakem križišču, na koncu dobimo:
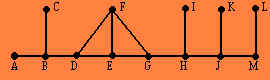
Iz središča labirinta, označenega z A, pa do izhoda, označenega z M, lahko pridemo po poti ABDEGHJM, vse ostale prehode pa lahko enostavno izpustimo.
Sedaj pa si oglejmo pot, ki se začne v sredini in nas pripelje do izhoda v poljubnem labirintu. Pravzaprav iščemo sprehod, ki vsebuje vse povezave pripadajočega grafa, saj mora tak sprehod obiskati tako sredino, kot tudi izhod iz labirinta. Če je graf povezan, se da tak sprehod vedno najti. O tem se lahko preprosto prepričamo, če vsako povezavo zamenjamo z dvojno (z dvema povezavama). V tako dobljenem grafu imajo vse točke sodo stopnjo in zato v grafu Eulerjev obhod obstaja. Torej v originalnem grafu obstaja sprehod, ki vsako povezavo prehodi natanko dvakrat, kar smo tudi želeli.
S tem pa smo na žalost samo dokazali, da rešitev (izhod iz labirinta) res obstaja, ne pa tudi kakšna je postopek (pot), ki nas do nje privede.
Najboljši algoritem za rešitev iz labirinta je objavil Gaston Tarry leta 1895. Njegova metoda pa temelji na naslednjem pravilu: nikoli se ne vrni po povezavi, ki je prva pripeljala do križišča, razen, če ni druge možnosti.
Če se tega pravila v labirintu držimo, bomo našli izhod iz povezanega labirinta, ne da bi prehodili katerokoli povezavo v labirintu več kot dvakrat (v vsaki smeri enkrat). Edina težava, ki pri tem nastane je ta, da je težko ugotoviti, katera povezava je tista, ki nas je do križišča pripeljala prva. Vendar tudi za to obstajajo pravila, ki pravijo:
Ko prvič hodiš po povezavi, pusti dve oznaki pri vhodu in eno ali tri oznake pri izhodu, odvisno od tega, ali je bilo križišče obiskano prvič ali ne.
Ko vstopiš na povezavo, označeno z eno oznako, pustiš ob njej še drugo oznako.

Stema dvema praviloma lahko takoj ugotovimo, katera povezava je bila že prehojena in katera še ne:
Brez oznake: povezava še ni bila prehojena, zato jo lahko uporabimo;
Ena oznaka: povezava je bila prehojena pri prihodu v križišče, zato jo lahko uporabimo za pot iz križišča;
Dve oznaki: povezava je bila že uporabljena za izhod iz križišča, zato je v tej smeri ne smemo več uporabiti;
Tri oznake: to je povezava, s katero smo prvič prišli v križišče, zato jo lahko uporabimo samo, če v križišču ni nobene povezave brez ali z eno oznako.
Tako lahko s pomočjo teh pravil pridemo iz vsakega labirinta, ne da bi prehodili katerokoli povezavo več kot dvakrat (po enkrat v vsako smer).