Darts
Deze Java-applet benadert het getal pi=3.1415926... door middel van
pijltjes gooien.
 Indien
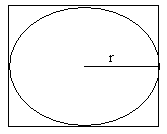
we de oppervlakte van een cirkel met straal r (dit is pi×r²) vergelijken
met die van een een vierkant met zijde 2r (zie tekening) dan kunnen we
pi benaderen door random pijltjes te gooien in het vierkant. De verhouding
(aantal pijlen terecht gekomen in cirkel)/(totale aantal gegooid) zal bij
benadering pi/4 zijn. Hoe langer we gooien hoe beter de benadering zal
zijn.
Indien
we de oppervlakte van een cirkel met straal r (dit is pi×r²) vergelijken
met die van een een vierkant met zijde 2r (zie tekening) dan kunnen we
pi benaderen door random pijltjes te gooien in het vierkant. De verhouding
(aantal pijlen terecht gekomen in cirkel)/(totale aantal gegooid) zal bij
benadering pi/4 zijn. Hoe langer we gooien hoe beter de benadering zal
zijn.
Betrouwbaarheidsintervallen
De vraag die we ons natuurlijk meteen stellen is: hoe goed is nu deze
benadering van pi? Als statistici denken we dan aan betrouwbaarheidsintervallen.
Het kansmodel dat we hiervoor gebruiken is de binomiale verdeling.De pijl
komt met kans p in de cirkel, en met kans q=1-p buiten de
cirkel. Na n keer gooien is de verwachting van het aantal pijlen
dat binnen de cirkel terecht is gekomen: np en de variantie van
deze grootheid is npq. Het 95% betrouwbaarheidsinterval voor de
schatter van p: (het aantal terecht gekomen binnen de cirkel)/(het
totale aantal pijlen gegooid), is als volgt:
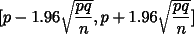
waarbij p de schatting is, q=1-p en n het aantal
malen gegooid. Vermenigvuldigen met 4 levert het betwrouwbaarheidsinterval
voor pi op.
Gebruiksaanwijzing
Het aantal worpen kan met een menu ingesteld worden (let op: n>10000
kan lang duren). Na "Start" wordt er gegooid, en betrouwbaarheidintervallen
na n/4, n/2, 3/4n, n worden getoond.
Source
De Java-source van deze applet kan bekeken
en gekopieerd worden.
Credits
De wiskundige formule van het betrouwbaarheidsinterval is gemaakt met
tex2gif op werkstations van GAMS Development Corp, Washington DC. De achtergrond
is afkomstig van een Web-pagina van een dartliefhebber (sorry, ik ben vergeten
wie.... Ik zal weer eens gaan zoeken en netjes om toestemming vragen).
De tekst is opgemaakt met Netscape Gold, met wat handmatige bewerkingen
achteraf.
De applet is ontwikkeld met Symantec Cafe.
Erwin Kalvelagen, CBS RSI, ekln@cbs.nl
 Indien
we de oppervlakte van een cirkel met straal r (dit is pi×r²) vergelijken
met die van een een vierkant met zijde 2r (zie tekening) dan kunnen we
pi benaderen door random pijltjes te gooien in het vierkant. De verhouding
(aantal pijlen terecht gekomen in cirkel)/(totale aantal gegooid) zal bij
benadering pi/4 zijn. Hoe langer we gooien hoe beter de benadering zal
zijn.
Indien
we de oppervlakte van een cirkel met straal r (dit is pi×r²) vergelijken
met die van een een vierkant met zijde 2r (zie tekening) dan kunnen we
pi benaderen door random pijltjes te gooien in het vierkant. De verhouding
(aantal pijlen terecht gekomen in cirkel)/(totale aantal gegooid) zal bij
benadering pi/4 zijn. Hoe langer we gooien hoe beter de benadering zal
zijn.